-
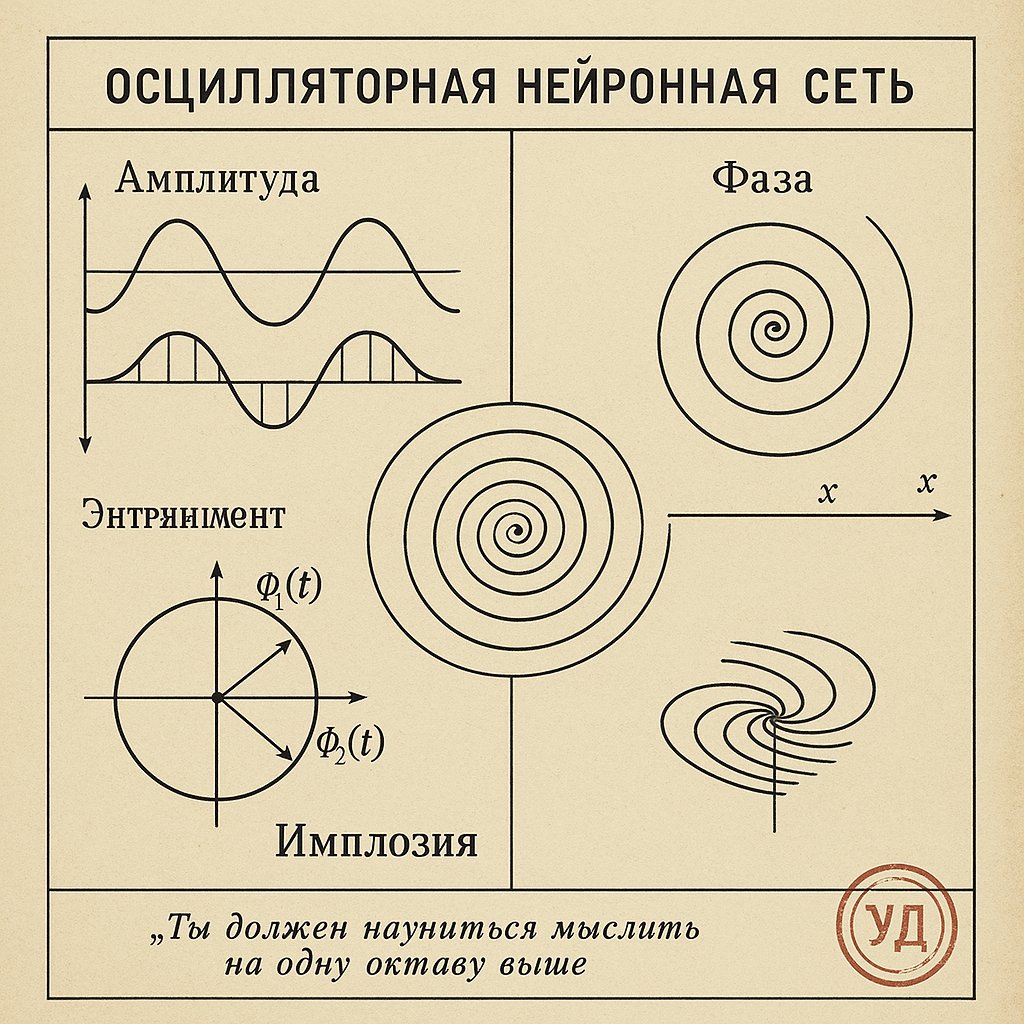
Oscillatory Neural Networks (ONNs) Key Terms
In oscillatory neural networks (ONNs), several key terms and parameters define the dynamics and behavior of the system. Here’s a comprehensive list of the most important ones, including ω (omega) and their roles:
1. Core Parameters & Variables
ω (Omega) – Angular Frequency
- Defines the natural oscillation rate of a neuron or oscillator.
- Units: radians per second (rad/s).
- Higher ω → faster oscillations.
θ (Theta) – Phase
- Represents the current position in the oscillation cycle (0 to \(2\pi\)).
- Dynamics: \( \frac{dθ_i}{dt} = \omega_i + \text{coupling terms} \).
A (Amplitude)
- The magnitude of oscillation (e.g., spike height in neural models).
- Sometimes dynamic (e.g., in amplitude death phenomena).
φ (Phi) – Phase Difference
- Relative phase between two oscillators (\( \phi = \theta_j - \theta_i \)).
- Critical for synchronization.
2. Coupling & Interaction Terms
K (Coupling Strength)
- Determines how strongly oscillators influence each other.
- High \( K \) → faster synchronization.
J (Connection Weights)
- Synaptic-like weights between oscillators (e.g., \( J_{ij} \) for neuron \( i \leftarrow j \)).
g(φ) – Phase Response Curve (PRC)
- Describes how an oscillator’s phase shifts due to input.
3. Synchronization & Collective Dynamics
Sync Order Parameter (R)
- Measures global synchronization:
\[
R e^{i\psi} = \frac{1}{N} \sum_{j=1}^{N} e^{i\theta_j}
\] - \( R \approx 1 \): Perfect sync; \( R \approx 0 \): No sync.
Critical Coupling (Kₐ)
- Threshold coupling strength for synchronization (e.g., in Kuramoto model).
Cluster States
- Subgroups of oscillators sync separately (e.g., phase-locked clusters).
4. Noise & Disturbances
D (Noise Intensity)
- Adds stochasticity (e.g., \( \frac{dθ*i}{dt} = \omega_i + \xi_i(t) \), where \( \langle \xi_i(t) \xi_j(t’) \rangle = 2D \delta{ij} \delta(t-t’) \)).
Hysteresis
- Memory-dependent effects under parameter changes.
5. Network Structure Terms
Topology
- Defines connectivity (e.g., all-to-all, small-world, scale-free).
Delay (τ)
- Time lag in interactions (e.g., \( \sin(\theta_j(t-\tau) - \theta_i(t)) \)).
6. Special Models & Extensions
- Kuramoto Model: \( \frac{dθ_i}{dt} = \omega_i + \frac{K}{N} \sum \sin(\theta_j - \theta_i) \).
- Stuart-Landau Oscillators: Complex amplitudes with \( \dot{z} = (\lambda + i\omega)z - |z|^2z \).
- Hopf Oscillators: Used in central pattern generators (CPGs).
7. Biological Analogies
- Gamma/Beta Bands: Frequency ranges (e.g., 30-100 Hz gamma oscillations in cognition).
- Spike-Phase Coding: Info encoded in spike timing relative to oscillation phase.
Summary Table
Term Symbol Role Angular Frequency ω Sets oscillation rate Phase θ Position in cycle Coupling Strength K Sync control Order Parameter R Sync measure Noise D Stochastic effects Connection Weight J_{ij} Network influence Phase Response Curve g(φ) Phase shift dynamics -
In science, if the experiment works and can be reproduced, the path you took barely matters. Beware the high priest who tells you otherwise.

-
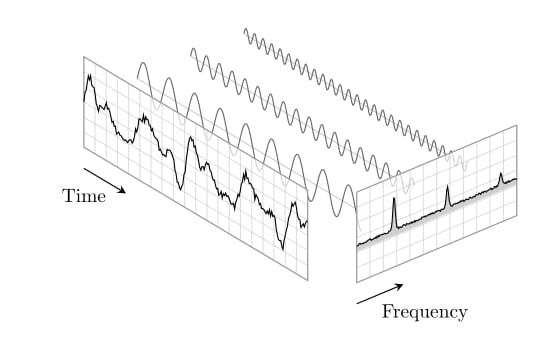
Pink Noise - The "1/f" structure of spectral brain dynamics
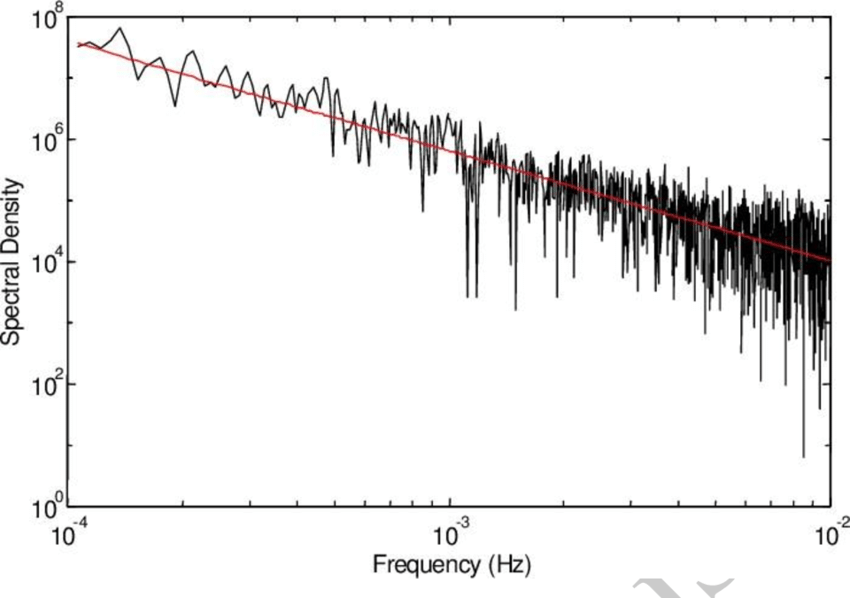
1/f noise, also known as flicker noise or pink noise, is a type of noise where the power spectral density is inversely proportional to the frequency. This means the noise power decreases as the frequency increases. 1/f noise is observed in various fields, including electronics, music, biology, and economics
James Keeler and Farmer demonstrated that a system of coupled logistic maps could produce fluctuations with a 1/f power spectrum. They showed that this occurred because the system continually tunes itself to stay near a critical point, a property that was later dubbed self-organized criticality by Per Bak. - Source
-
LLMs are revolutionizing science education. For any topic, you can now generate interactive explanations, adapt them in real time, and play with them until it clicks. Underrated.
-
Oscillatory Mycelium - Overview
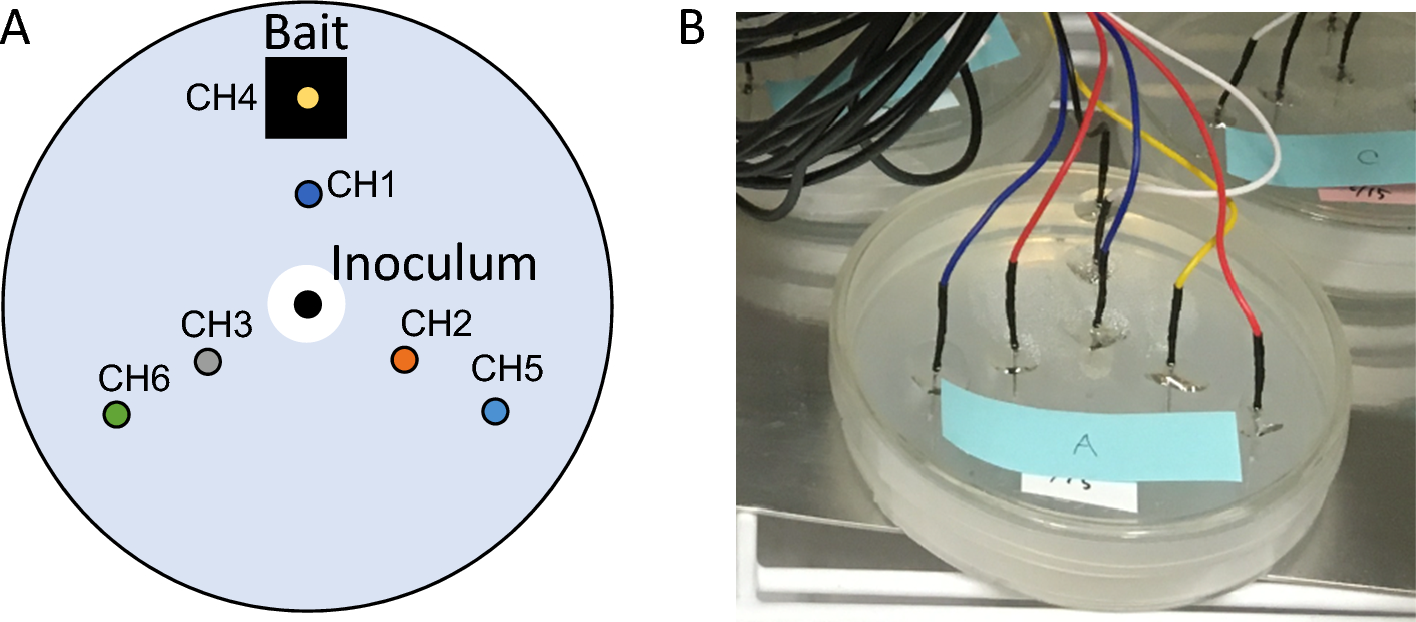
1. Oscillatory Growth:
- Hyphae, the thread-like filaments of fungi, don't grow at a constant rate. Instead, they exhibit oscillations in growth speed.
- These oscillations are thought to be related to changes in the hyphal tip, including the fusion of vesicles with the plasma membrane and dynamic changes in the cell wall's mechanical properties.
- These oscillations in growth are linked to fluctuations in turgor pressure, which is the pressure within the hyphal cell.
- Research has even shown that these growth oscillations can be synchronized between hyphae, preparing them for fusion, according to eLife.
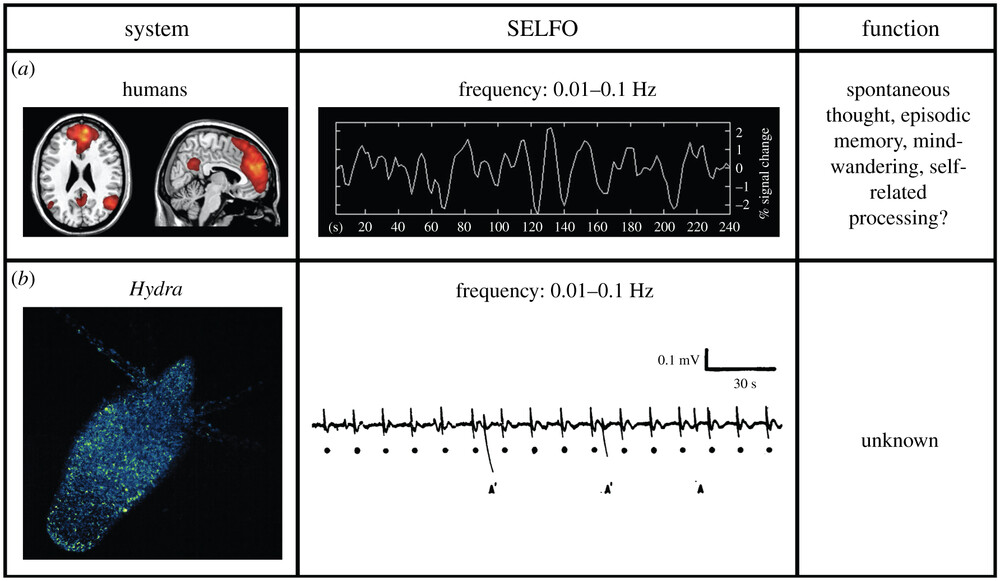
2. Oscillatory Electrical Potential:
- Fungal mycelia can exhibit spontaneous electrical low-frequency oscillations (SELFOs).
- These oscillations have been detected throughout the mycelial network and may serve as a form of communication.
- One study even recorded a week-long electrical oscillation in the mycelium of a wood decay fungus, according to Tohoku University.
3. Oscillatory Pattern Formation:
- Some studies have shown that oscillations can contribute to the formation of patterns within the mycelial network.
- For example, the growth of mycelium on a substrate can lead to the emergence of spatially organized oscillatory domains.
4. Significance:
Understanding oscillatory mycelium can provide insights into how fungal mycelia communicate, coordinate growth, and respond to environmental stimuli.
It can also have implications for our understanding of fungal development, disease, and the use of mycelium in biotechnology.
Links:
https://pubmed.ncbi.nlm.nih.gov/29229585/
https://royalsocietypublishing.org/doi/10.1098/rsif.2024.0574
https://sciencedirect.com/science/article/pii/S0303264723001089
https://ieeexplore.ieee.org/document/10628662
-
Fractal Turtles All The Way Down

The shells of many species of turtles and tortoises are intricately marked and colored, yet are perfectly designed by nature to blend precisely with their natural habitats.
Check the species shown in the image, respectively:
– Top row, from left to right:
1) Eastern box turtle (Terrapene carolina carolina);
2) Pancake turtle (Malacochersus tornieri);
3) Bell tortoise (Kinixys belliana);
– Middle line from left to right:
4) Irradiated turtle (Astrochelys radiata);
5) Florida box turtle (Terrapene carolina bauri);
6) Burmese star turtle (Geochelone platynota);
– Bottom line from left to right:
7) Spotted turtle (Clemmys guttata);
8) Bourret's box turtle (Cuora bourreti);
9) Striated shell turtle (Emys orbicularis).
📸 Photos by Garden State Tortoise