PhaseScope – The Oscillatory Network Microscope
Samim.A.Winiger - 12.May.2025
Abstract
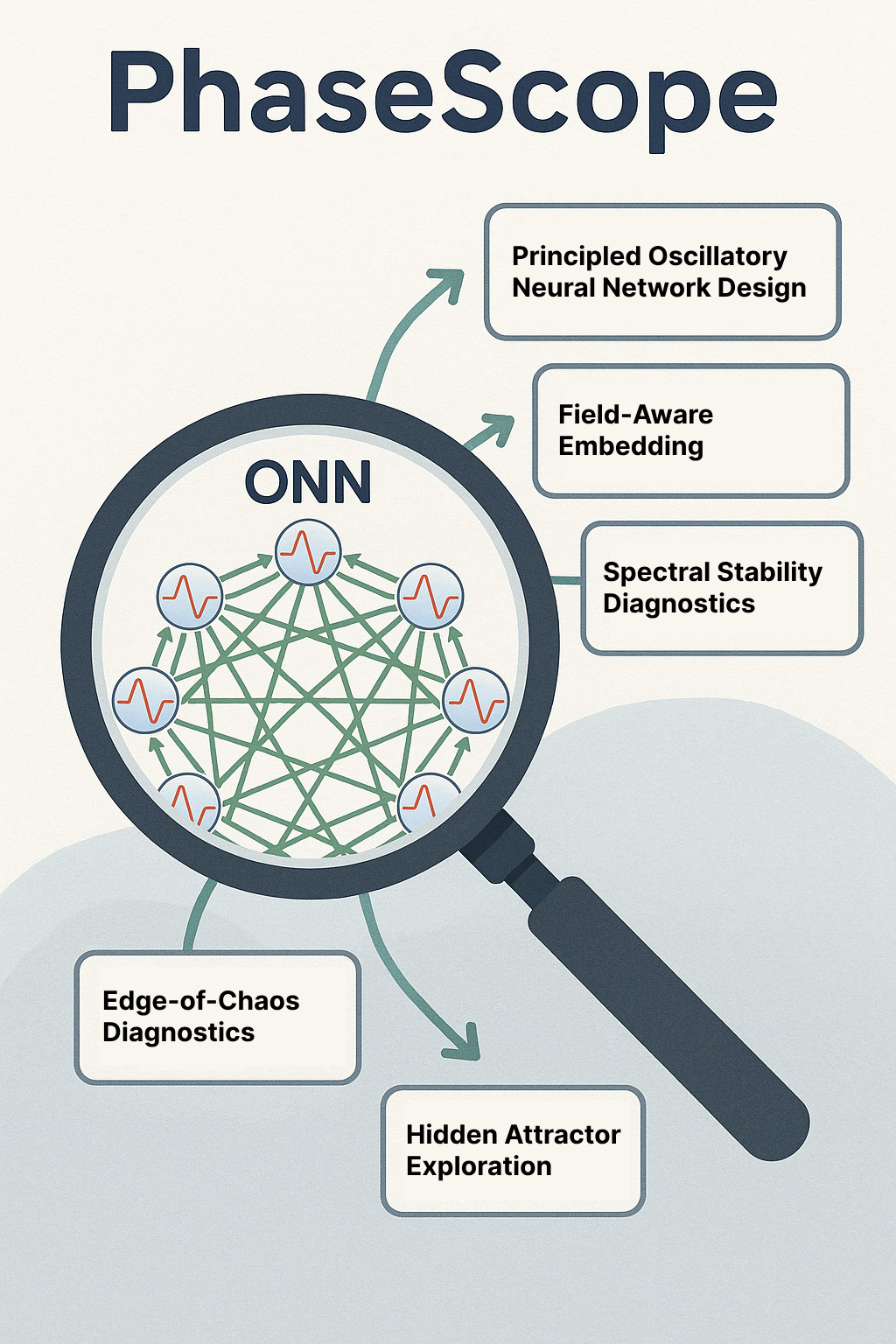
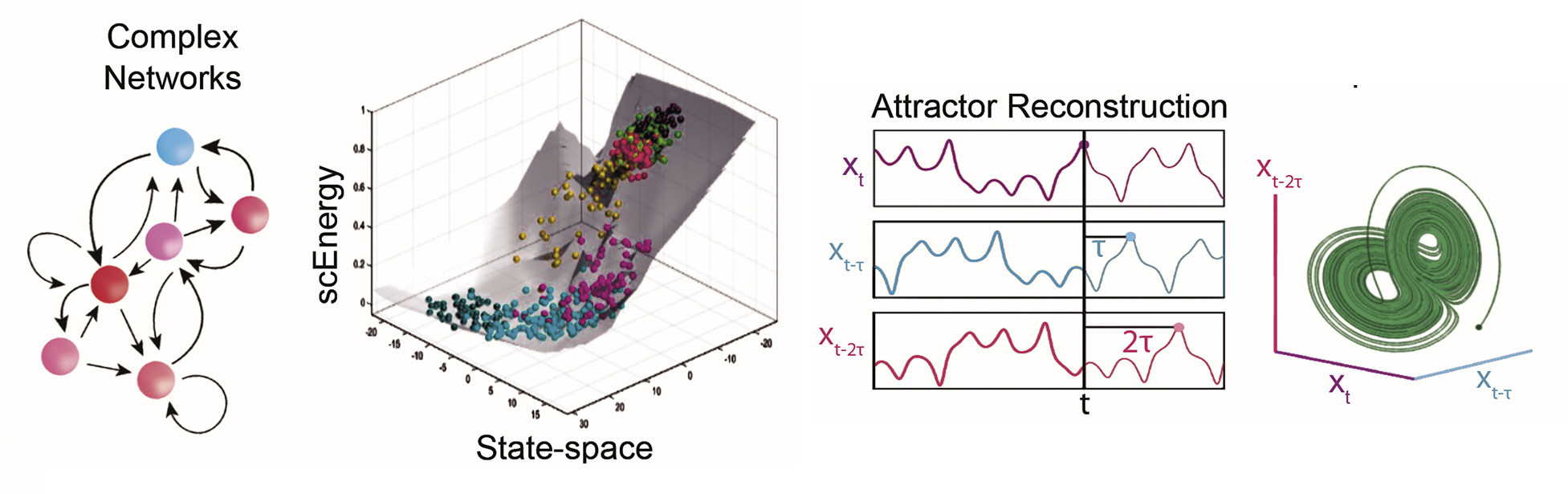
Oscillatory neural networks (ONNs) hold significant promise for advanced AI, yet their complex internal dynamics impede robust design and verification. Current analytical tools often fall short in providing rigorous stability guarantees and comprehensive, interpretable insights for these systems. This paper introduces PhaseScope, a theoretical framework and computational toolkit designed to bridge this gap. PhaseScope integrates three core pillars: (1) a novel field-aware embedding theory for reconstructing high-dimensional attractors from distributed neural activity; (2) advanced spectral stability diagnostics for spatio-temporal patterns; and (3) systematic methods for active hidden-attractor exploration.
By combining these advances, PhaseScope aims to establish stronger theoretical foundations and reliable diagnostic tools for the principled design, analysis, and deployment of Oscillatory Neural Networks.
1. Introduction
Oscillator-based networks, utilizing phase-encoding and coupled oscillatory dynamics, offer significant potential for advanced AI applications. However, a comprehensive understanding of their internal dynamics, particularly in spatially extended architectures, remains a critical challenge. While numerous powerful analytical tools exist for dynamical systems and machine learning (including operator-theoretic methods, manifold learning, and TDA, as discussed in Sec. 5.5), the application of rigorous dynamical systems tools (like state-space reconstruction and detailed stability analysis) to understand the internal workings and ensure the robustness of ONNs used in AI is still an emerging area. Current approaches, when applied in isolation or heuristically to these specialized networks, can face limitations in providing verifiable stability margins, comprehensive hidden-mode discovery, and clear paths to interpretable, robust design.

This proposal introduces PhaseScope, a theoretical framework and computational toolkit designed to address this gap by providing the necessary "microscope" to bridge functional performance with fundamental dynamical understanding. PhaseScope integrates three core components:
- A novel field-aware embedding theory to reconstruct attractors from spatially distributed neural activity.
- Robust spectral analysis techniques for analysis of spatio-temporal pattern stability and network complexities.
- Systematic methods for active hidden-attractor exploration.
The overarching objective is to establish a unified methodology that moves beyond heuristic approaches, providing stronger theoretical foundations and reliable diagnostic tools for the principled design, verification, and trustworthy deployment of oscillator-based AI systems.
2. Guiding Philosophy
As machine learning researchers enthusiastic about the potential of oscillatory AI, we approach the advanced mathematics and nonlinear dynamics involved with a “beginner’s mind"—echoing Zen master Shunryu Suzuki’s insight that “in the beginner’s mind there are many possibilities, but in the expert’s there are few”. This spirit fuels our commitment to hands-on exploration, to learning by building, and critically, to making these complex systems and their sophisticated analysis more accessible to a broader range of practitioners.
3. Key Contributions
PhaseScope’s key contributions to the analysis of oscillator-based neural networks include:
- Novel Field-Aware Embedding Theory: For reconstructing dynamics from spatially distributed, noisy sensor data, extending classical theorems.
- Advanced Spectral Stability Diagnostics: Applying Floquet-Bloch theory and other spectral methods for robust stability analysis of diverse spatio-temporal patterns.
- Systematic Hidden-Attractor Exploration: A framework using intelligent probing to discover elusive dynamical regimes and potential failure modes.
- Edge-of-Chaos Diagnostics: Metrics and alerts to identify and help operate networks in computationally optimal regimes.
- An Integrated, Accessible Toolkit: A unified software platform implementing these theoretical advances to make them broadly accessible for “white-box” understanding.
4. Motivation & Vision
4.1. The Rising Importance and Current Challenges of Oscillator-Based Neural Networks
Neural network architectures increasingly draw inspiration from neurobiological principles, among which oscillatory dynamics and phase-based information encoding are particularly prominent. Oscillator-based neural networks offer compelling advantages for artificial intelligence tasks, including robust temporal sequence representation and efficient rhythm tracking, lending themselves to potentially more energy-efficient and dynamically rich computational models.
Despite their promise, the widespread adoption of these networks is hampered by the opaque nature of their internal dynamics. As networks are trained, they can settle into complex operational regimes. Understanding _how_ they compute or _why_ they succeed or fail often remains elusive. This “black-box” character leads to practical pain points: brittle training, unpredictable performance, undetected failure modes (hidden attractors that compromise reliability), and significant difficulties in verification and validation for critical applications.
4.2. The PhaseScope Vision: From Opaque Dynamics to Robust Analytical Foundations
The vision for PhaseScope is to address these critical challenges by providing a rigorous, data-driven “microscope” for the design, diagnosis, and control of oscillator-based neural networks. We aim to move the field beyond heuristic approaches towards a paradigm where the behavior of these systems can be understood and predicted with enhanced confidence and stronger theoretical backing. PhaseScope endeavors to equip researchers and engineers with tools to illuminate internal workings, enable principled design, and ensure more trustworthy AI by transforming trained oscillator networks into more transparent systems.
Ultimately, we envision PhaseScope as part of a broader framework that does for oscillator-based AI systems what PyTorch did for differentiable programming: offering an integrated, principled toolkit that translates theoretical insights into practical design and analysis tools.
5. Background & Related Work
The PhaseScope framework builds on dynamical systems theory, time-series analysis, and computational science, extending established methods to address the unique challenges of oscillator-based neural networks (ONNs) and their current analytical limitations.
5.1. Embedding Theory from Single Time Series
The reconstruction of a system’s attractor from observed time series data using delay coordinates is a cornerstone of nonlinear dynamics.
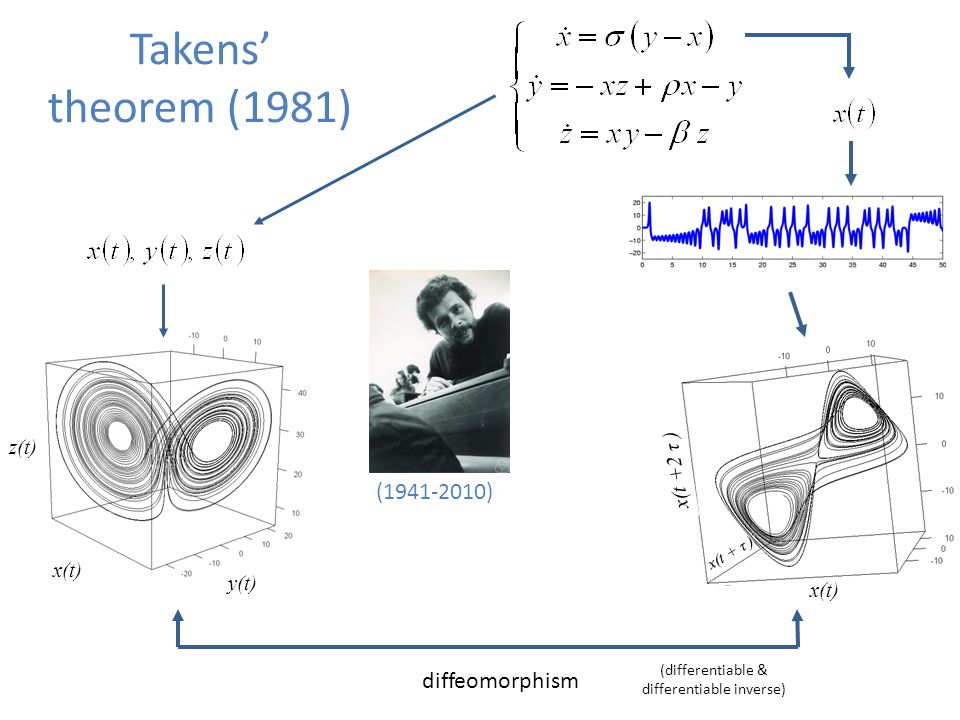
Takens’ theorem (1981) provided a foundational guarantee that for a generic smooth observation \(h\) and flow \(\Phi^t\) on a compact \(d\)-dimensional manifold, the delay-coordinate map is an embedding if the embedding dimension \(m > 2d\) (Takens 1981).
"Embedology" (Sauer, Yorke & Casdagli, 1991) extended this to fractal attractors, establishing the embedding bound \(m > 2d{A}\) (where \(d{A}\) is the box-counting dimension), critical for complex attractors in neural systems (Sauer et al. 1991).
Practical limitations: While Takens’ theorem and its extensions provide a powerful theoretical foundation, their practical application is subject to important constraints. Embedding-based reconstructions are highly sensitive to measurement noise, and even moderate noise can severely degrade attractor reconstruction and parameter estimation (Casdagli et al., 1991). The amount of data required for reliable embedding increases rapidly with the effective dimensionality of the system (Eckmann & Ruelle, 1992), making high-dimensional or weakly synchronized systems especially challenging. Methods for selecting embedding parameters (such as delay and dimension) are heuristic and can be unstable in noisy or short datasets. Moreover, colored noise and certain stochastic processes can produce apparent attractor-like structures, complicating the distinction between genuine low-dimensional chaos and random dynamics (Osborne & Provenzale, 1989; Provenzale et al., 1992).
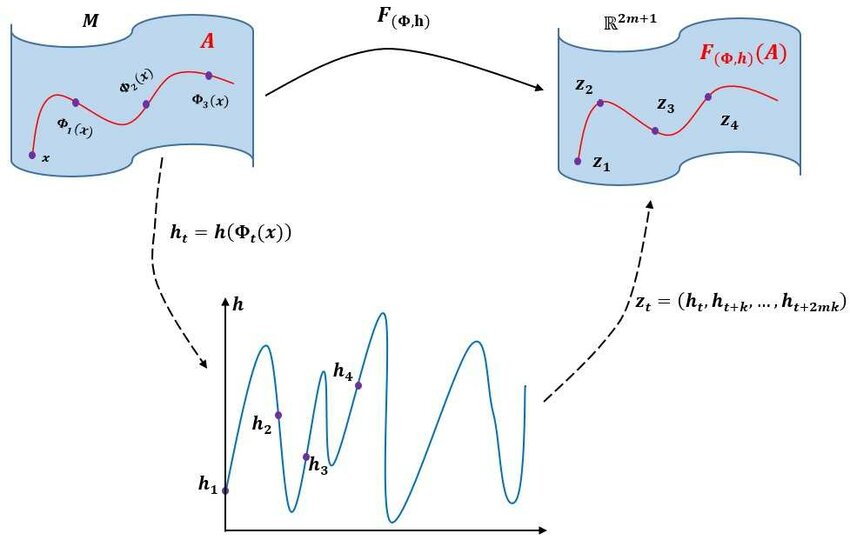
5.2. Embedding Spatially Distributed Dynamics & Infinite-Dimensional Systems
While classical embedding theory predominantly addresses scalar time series, oscillator networks generate field-valued data. Reconstructing dynamics from such data requires significant extensions.
- Work on infinite-dimensional extensions of embedding theory, notably by Robinson (2005), demonstrated that flows on Hilbert-space attractors with finite box-counting dimension can be embedded using delay-coordinate maps (Robinson 2005). This, and related work on approximate inertial manifolds for systems with delay (e.g., Rezounenko 2003), provides a vital theoretical bridge for systems like PDEs and large-scale oscillator networks. The influence of noise on such embeddings, particularly in forced systems, is an important consideration (e.g., Stark et al. 2003).
- However, a key open challenge is proving that a minimal set of pointwise sensors (or limited spatial modes), combined with time delays, can ensure a faithful reconstruction for such spatially extended systems, especially under noisy conditions. Recent developments in multi-channel embedding theorems (e.g., Kukavica & Robinson 2004) and specific research on the embedding of neural fields are highly relevant to this challenge and inform PhaseScope’s approach.

5.3. Floquet-Bloch Analysis and Broader Spectral Approaches
Understanding the stability of periodic behaviors is crucial. Floquet theory provides a rigorous framework for ODEs with time-periodic coefficients (Nayfeh & Balachandran 1995, Ch. 7).
- For spatially extended systems with spatio-temporal periodicity (e.g., wave patterns in lattice-structured networks), this generalizes to Floquet-Bloch analysis, incorporating Bloch’s theorem from solid-state physics (Rabinowitz 2000, Sec. 8.4). The emergence of complex patterns like chimera states in such networks (Panaggio & Abrams 2015) further underscores the need for robust spatio-temporal stability analysis. The specific application of Floquet theory to neural oscillators (e.g., Rugh et al. 2015) and the known challenges of applying Floquet-Bloch theory to complex networks (e.g., Pecora & Carroll 1998, particularly regarding the Master Stability Function for networked systems, which typically applies to identical oscillators and doesn’t directly handle all spatial wave patterns; Strogatz 2000 for general reference on disorder in networks) are important considerations addressed by PhaseScope.
5.4. Hidden Attractors
A hidden attractor is one whose basin of attraction does not intersect with small neighborhoods of equilibria, distinguishing them from “self-excited” attractors (Leonov & Kuznetsov 2013; Kuznetsov et al. 2015).
- Their existence can lead to unexpected behaviors or failure modes. Standard simulation protocols often miss them. More recent surveys and methods have advanced the techniques for finding and characterizing hidden attractors in various dynamical systems (e.g., Kuznetsov, Leonov & Mokaev 2015; Pisarchik & Feudel 2014).
5.5. Complementary Methodologies
- Operator-Theoretic Approaches (Koopman/DMD) (Mezić 2005; Schmid 2010; Brunton et al. 2016)
- Manifold Learning (e.g., Diffusion Maps) (Coifman & Lafon 2006)
- Topological Data Analysis (TDA, e.g., Persistent Homology) (Edelsbrunner & Harer 2010)
- General Active Basin Exploration & Perturbation Methods (e.g., Jones et al. 2001)
6. The PhaseScope Framework
The PhaseScope framework is engineered to provide a comprehensive, multi-faceted analysis of oscillator-based neural networks. It rests upon three synergistic core pillars, each addressing a critical aspect of understanding and characterizing these complex dynamical systems. These pillars are designed to work in concert, moving from data acquisition and state-space reconstruction to stability analysis and the exhaustive mapping of all relevant dynamical regimes.
6.1. Core Pillars
6.1.1. Field-Aware Delay Embedding
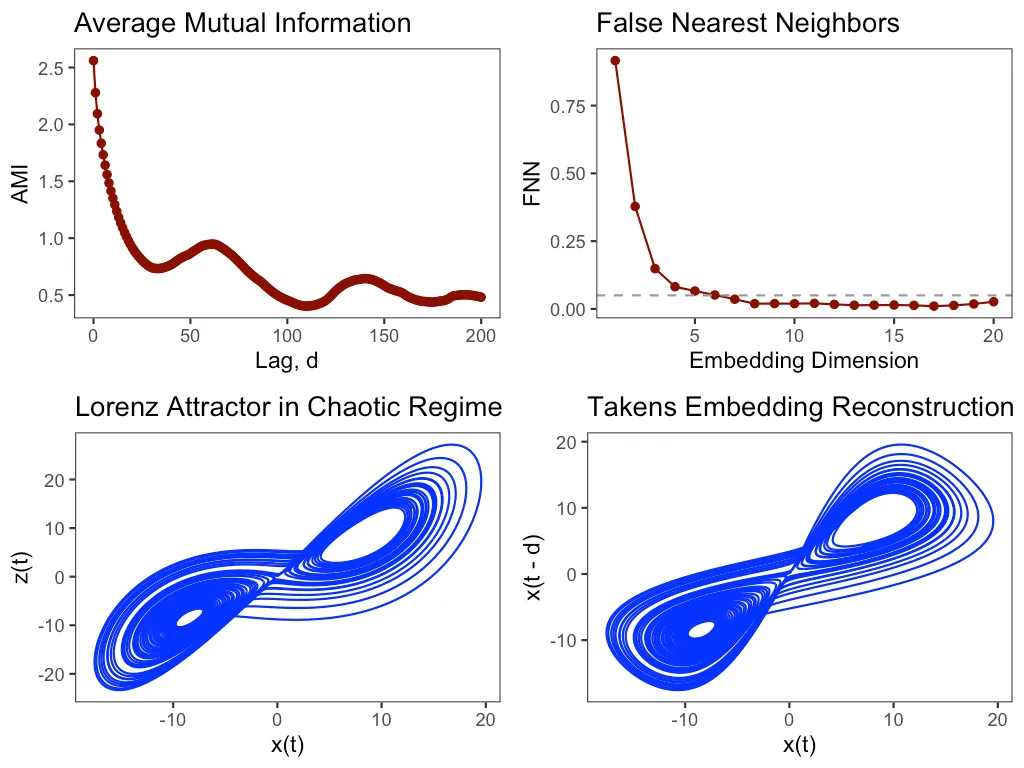
The first pillar focuses on reconstructing the system’s high-dimensional attractor from spatially distributed observations using a novel field-aware embedding theory (detailed in Section 6.2.1). This involves capturing sufficient information from selected sensor channels to represent the state of the oscillator network faithfully. Practical selection of the delay \(\tau\) and per-channel embedding dimension \(m_{ch}\) will be guided by established methods adapted for multi-channel data, such as mutual information and false near-neighbor analysis (further detailed in the EmbedExplorer module, Section 6.3.2). The goal is to produce a reliable geometric representation of the system’s dynamics, which forms the foundation for subsequent analysis by the other pillars.
6.1.2. Spectral Stability Diagnostics and Analysis
The second pillar focuses on rigorously assessing the stability of periodic and spatio-temporally periodic operational modes identified within the oscillator network. Many functional states in these networks, such as those responsible for generating rhythmic patterns, maintaining clock-like oscillations, or representing entrained responses, are inherently periodic or involve repeating spatial patterns that evolve periodically in time. This pillar leverages Floquet-Bloch theory for systems with appropriate symmetries, and extends to a broader suite of spectral tools (including Lyapunov exponent analysis) for more general network structures and dynamics, as detailed in Section 6.2.3. This pillar is vital for understanding the robustness of desirable functional states. It seeks to provide well-grounded stability margins, indicating how susceptible a given operational mode is to noise, parameter drift, or input perturbations, thereby informing network design for enhanced reliability.
6.1.3. Edge-of-Chaos Flagging and Adaptive Tuning
SpectraLab will continuously monitor the network’s proximity to critical dynamical boundaries by tracking key indicators (e.g., Lyapunov exponents nearing zero, Floquet multipliers approaching unity, or topological changes detected by TopoTrack). Recognizing that precise “edge-of-chaos” thresholds are system-dependent and a research challenge [cf. Bertschinger & Natschläger 2004], PhaseScope will provide diagnostics and alerts based on these indicators. When alerts suggest the system is nearing instability or excessive order, PhaseScope aims to facilitate (and potentially automate) cautious, iterative tuning of relevant network parameters (like global coupling or noise levels). This aims to maintain computationally rich dynamics while preventing collapse, leveraging efficient stability assessment methods (e.g., Krylov subspace techniques [cf. Lehoucq et al. 1998]) for scalability.
6.1.4. Active Hidden-Attractor Exploration
The third pillar is dedicated to the systematic discovery and characterization of hidden attractors. These are stable dynamical regimes whose basins of attraction do not connect to any obvious equilibria or easily found periodic orbits. Standard simulation approaches, typically initiated from random states or quiescent conditions, may entirely miss these hidden modes, which can represent latent failure states, unexpected operational capabilities, or transitions to undesirable behaviors.
PhaseScope’s Active Hidden-Attractor Exploration will employ:
- Intelligent State-Space Probing: Rather than relying on purely random initializations, this approach will use information gleaned from the reconstructed embedding space (via Pillar 6.1.1) and local stability analyses (via Pillar 6.1.2) to guide the search, leveraging strategies akin to efficient global optimization (e.g., Jones, Schonlau & Welch 2001). For instance, perturbations can be targeted towards regions of the embedding space that are sparsely populated by observed trajectories or near points of marginal stability.
- Data-Driven Basin-Sampling Techniques: Methods will be developed to systematically sample the high-dimensional state space of the network, potentially using adaptive strategies or heuristics inspired by global optimization or rare-event sampling methods (e.g., importance sampling).
- Perturbation Engines: Controlled perturbations will be applied to the network during operation or simulation to attempt to “kick” the system into the basins of attraction of hidden modes, potentially employing principles from control theory for steering trajectories (e.g., Ott, Grebogi & Yorke 1990).
The scientific importance of this pillar lies in its potential to provide a far more complete picture of a network’s dynamical landscape than is typically achieved. By actively seeking out these elusive “dark” regimes, PhaseScope aims to identify potential vulnerabilities or unexploited capabilities, contributing to the safety, robustness, and overall trustworthiness of oscillator-based AI. While comprehensively mapping all basins in high-dimensional systems can be computationally prohibitive (potentially exponential complexity), these heuristic methods aim to significantly improve discovery efficiency in practice.

6.2. Theoretical Foundations
The PhaseScope framework’s analytical rigor stems from adapting established mathematical principles and introducing specific theoretical advancements. These foundations underpin the methodologies in each core pillar (Section 6.1), enabling robust analysis tailored to the unique challenges of spatially extended, nonlinear oscillator networks and aiming for deeper insights.
6.2.1. Towards a “Neural Takens” Theorem: Embedding Spatially Distributed Oscillator Dynamics
The cornerstone of our Field-Aware Delay Embedding pillar is the formulation and rigorous investigation of a "Neural Takens” Theorem, tailored for spatially extended oscillator networks. This endeavor explicitly builds upon classical embedding theory, which requires certain prerequisites: the system’s dynamics must be smooth and evolve on a compact attractor, the observation function must be generic (in a Ck sense, meaning its derivatives up to order k are continuous and well-behaved), and the embedding dimension must be sufficiently high (Whitney, 1936; Takens, 1981; Sauer et al., 1991).
Building on Foundations: Classical Takens’ theorem (Takens, 1981) established that for a \(d\)-dimensional smooth attractor, a delay-coordinate map from a _generic_ scalar observation function forms an embedding if the embedding dimension \(m > 2d\). Whitney’s embedding theorem (Whitney, 1936) provides an even earlier conceptual basis, showing a \(d\)-manifold embeds in \(\mathbb{R}^{2d+1}\). Sauer et al. (1991) extended these ideas to fractal attractors. Robinson (2005) further generalized embedding concepts to infinite-dimensional systems possessing finite-dimensional attractors. Our work directly addresses the critical next step: extending these guarantees to practical, multi-channel observations from spatially distributed neural fields. This involves drawing from recent advancements in multi-channel embedding theorems (e.g., Kukavica & Robinson 2004) and embedding techniques specifically for neural fields. A central challenge, which PhaseScope aims to address, is the impact of observational and system noise (Stark et al., 2003), ensuring robust embedding under realistic conditions.
Inertial Manifold Hypothesis & Genericity in Neural Networks: A key working hypothesis is that the complex dynamics of many relevant oscillator network models (e.g., coupled Kuramoto oscillators (Kuramoto, 1984), FitzHugh-Nagumo arrays, certain classes of recurrent neural networks) effectively evolve on an \(N\)-dimensional inertial manifold \(\mathcal{M}\), despite their high nominal dimensionality (see Temam, 1997 for general background on inertial manifolds, particularly in the context of infinite-dimensional systems). Establishing or verifying conditions for the existence and finite-dimensionality of such manifolds for _trained_ oscillator networks, and clarifying how genericity conditions for embedding apply to neural oscillators with specific coupling symmetries, are important areas for detailed investigation within this framework.
The “Neural Takens” Conjecture for Multi-Channel Observations: We conjecture that a delay-coordinate map \(H_{\mathbf{P}, \tau, m_{ch}}\), constructed from \(P\) sensor channels (pointwise neuronal activity, local field potentials, or derived spatial modes \(\mathbf{y}_{k}(t)\)) with delay \(\tau\) and \(m_{ch}\) delays per channel (yielding a total embedding dimension \(m_{\text{total}} = P \times m_{ch}\)), forms an embedding of the system’s attractor \(\mathcal{A} \subset \mathcal{M}\) if \(m_{\text{total}} > 2 \dim_{B}(\mathcal{A})\). This formulation aligns with the classical \(> 2d_{A}\) requirement from Sauer et al. (1991) but explicitly leverages multiple synchronous observation streams. This approach is conceptually supported by work like Kukavica & Robinson (2004), who demonstrated that sufficiently many spatial point observations can embed a PDE’s attractor, and Robinson’s (2005) results on embedding infinite-dimensional systems using a large number of point measurements. The rigorous substantiation of this conjecture for ONNs, particularly concerning the interplay between \(P\), \(m_{ch}\), and \(\dim_{B}(\mathcal{A})\) in the context of neural field-like data and oscillator network characteristics, is a primary research goal of PhaseScope.
Spatio-Temporal Observability as a Linchpin: Crucially, the selection of sensor locations/modes \(\mathbf{P}\) is not arbitrary. It must satisfy a stringent _spatio-temporal observability condition_. This condition requires that the chosen set of sensors \(\mathbf{P}\), through their collective time-delayed measurements, can uniquely distinguish any two distinct states on the attractor \(\mathcal{A}\). Formally, this implies that the multi-channel observation function mapping states on \(\mathcal{A}\) to the sequence of measurements must be an immersion (i.e., its derivative is full rank), and for a compact attractor, this ensures an embedding (see, e.g., Guillemin & Pollack 1974 for the principle that an immersion from a compact manifold is an embedding). This moves beyond assuming a single scalar observation is _a priori_ generic in the sense of Takens (1981), instead focusing on ensuring the _chosen set_ of practically implementable sensors collectively provides sufficient information to distinguish neighboring states on the attractor. The necessity for multiple observation channels or carefully chosen single field measurements is underscored by known counterexamples in spatially extended systems (e.g., certain solutions to the complex Ginzburg-Landau equation can yield identical time series at a single spatial point, thereby failing to distinguish different spatial patterns). PhaseScope thus emphasizes multi-channel strategies designed to meet this observability demand, with robustness to noise being a key criterion for validating these strategies.
Addressing Genericity and Dimensionality: While the \(> 2 \dim_{B}(\mathcal{A})\) bound is standard for generic delay embeddings, its practical application to potentially very high-dimensional attractors in large networks necessitates careful consideration. Our investigation will link the required \(P \times m_{ch}\) to the complexity of _functional_ dynamics rather than merely network size, and explore how network architecture (e.g., sparse vs. dense connectivity, local vs. global coupling) influences \(\dim_{B}(\mathcal{A})\) and the satisfaction of observability conditions. Verifying that our proposed sensor configurations and the resulting observation functions meet the necessary genericity conditions for specific network architectures and sensor types will be a key research thrust, potentially leading to structural properties of the network rather than relying on abstract mathematical genericity alone.
The proof strategy for such a “Neural Takens” theorem will involve adapting techniques from differential topology and geometric measure theory, potentially including arguments related to the transversality of intersections for multi-sheeted embeddings arising from multi-channel observations, to specifically address the structured nature of \(H{\mathbf{P}, \tau, m{ch}}\) and the properties of attractors in common neural oscillator models.
6.2.2. Optimal Sensor Placement via Observability Gramian Analysis & Refinement
The practical utility of the “Neural Takens” theorem critically depends on selecting an effective, and ideally minimal, set of sensors. PhaseScope will develop a principled, adaptive strategy for sensor placement:
Linearized Observability as a Starting Point: We will initially leverage the Observability Gramian (\(\mathcal{W}_o\)) (see, e.g., Kailath 1980), computed from the linearized network dynamics around representative operational states (e.g., specific periodic orbits, or averaged dynamics over a typical trajectory segment if the system is chaotic). The goal is to select sensor locations/modes that maximize a robust metric of \(\mathcal{W}_o\) (e.g., its smallest eigenvalue, or a condition number related metric), thus ensuring local observability of all dynamical modes.
Computational Considerations: While powerful, the computation of the full Observability Gramian can scale as \(N^k\) or higher for networks of \(N\) oscillators if all cross-correlations are considered naively. A key aspect of SensorDesigner will be to investigate and implement computationally efficient approximations, explore methods leveraging network sparsity or structural properties (potentially inspired by methods for scalable Gramian computation, e.g., Obermeyer et al. 2018), and iterative refinement schemes to make optimal sensor placement tractable for large-scale networks.
Addressing Nonlinearity and Multiple Regimes:
- The initial placement based on \(\mathcal{W}_o\) serves as a well-founded starting point. Its effectiveness for the full nonlinear system will be validated empirically and potentially refined using nonlinear observability metrics or criteria that assess distinguishability across the empirically reconstructed attractor.
- For systems with multiple distinct operational regimes or attractors, sensor placement may need to be robust across these regimes, or an iterative approach may be employed: initial placement, partial attractor reconstruction, identification of poorly observed regions/dynamics, and sensor set refinement.
This layered approach to sensor selection aims to provide data that is rich enough for successful embedding, balancing theoretical rigor with computational feasibility.
6.2.3. Floquet–Bloch and Alternative Spectral Stability Analyses for Structured and Disordered Networks
PhaseScope’s stability analysis for spatio-temporal patterns will employ a formal Floquet-Bloch framework. It is crucial to acknowledge from the outset the foundational assumptions: classical Floquet theory applies to systems linearized around a strictly time-periodic orbit, yielding Floquet multipliers whose magnitudes determine stability (Nayfeh & Balachandran, 1995). Bloch’s theorem applies to systems with perfect spatial periodicity (e.g., crystal lattices), allowing solutions to be expressed as Bloch waves indexed by a wavevector \(\mathbf{q}\) (Rabinowitz, 2000). The combination, Floquet-Bloch analysis, is therefore rigorously applicable to determine the stability of spatio-temporal patterns that are periodic in both time and space within a perfectly regular lattice structure. The specific application of Floquet theory to neural oscillators (e.g., Rugh et al. 2015) and the challenges of extending Floquet-Bloch analysis to complex, non-ideal network structures (e.g., Pecora & Carroll 1998, particularly regarding the Master Stability Function for networked systems; Strogatz 2000 as a general textbook reference for disordered systems) are active areas of research that PhaseScope aims to contribute to and build upon.
Foundation & Ideal Cases: For network states \(\phi(\mathbf{x}_j, t)\) periodic in time \(T\) on an ideal spatial grid, linearization around a spatio-temporal orbit \(\phi_0(\mathbf{x}_j, t)\) yields a time-periodic linear system. If the grid possesses discrete translational symmetry, the Bloch transformation decouples this system into independent Floquet problems for each wavevector \(\mathbf{q}\) in the Brillouin zone. The resulting spatio-temporal Floquet multipliers \(\rho(\mathbf{q})\) (or exponents \(\lambda(\mathbf{q})\)) determine stability. This provides elegant analytical modes and a clear band structure for stability.
Relationship to Master Stability Function (MSF): For networks of coupled identical oscillators exhibiting a synchronized periodic state, the Master Stability Function (MSF) framework (Pecora & Carroll, 1998; Barahona & Pecora, 2002) provides a powerful and widely adopted method. The MSF approach decouples stability analysis along the eigenmodes of the network’s coupling matrix, effectively performing a Floquet analysis for each transverse mode. PhaseScope builds upon these foundational ideas, aiming to extend stability diagnostics to more complex spatio-temporal patterns (beyond simple synchrony) and to address non-identical oscillators or less regular structures where the classical MSF assumptions might be too restrictive.
Addressing Architectural Realities: Heterogeneity, Disorder, and Non-Periodic Dynamics:
Limitations and Adaptations: Real oscillator networks often deviate from ideal periodicity due to parameter mismatches, irregular connectivity (disorder), or by settling into quasi-periodic or chaotic attractors where Floquet exponents are not strictly defined (Lyapunov exponents become the relevant measure, as discussed in Section 6.1.2). In such cases, direct application of Floquet-Bloch theory is an approximation or a heuristic. When analyzing regimes that are not strictly periodic, PhaseScope will rely on Lyapunov exponent estimation (Section 6.1.2) rather than Floquet analysis for stability assessment. The stability of intricate patterns like chimera states (e.g., Rakshit et al., 2017), which can arise in such networks, requires careful consideration of these complexities.
Complex Symmetries & Disordered Systems: For networks with more complex symmetries than simple lattices, or with irregular topologies and quenched disorder (e.g., in couplings or intrinsic frequencies), true Bloch modes may not exist, and the concept of a \(k\)-vector becomes ill-defined. Here, PhaseScope will treat Floquet-Bloch analysis (when applicable to periodic states) as a heuristic spectral decomposition or revert to numerical eigen-decomposition of the full system Jacobian if a periodic orbit is identifiable. We will explore generalizations, potentially using concepts from equivariant bifurcation theory (e.g., Golubitsky & Stewart, 2002) or employing a spectral graph theory approach where eigenmodes of the graph Laplacian serve as a surrogate for Bloch modes for analyzing stability with respect to network structure (Panaggio & Abrams, 2015). It is important to note that even small deviations from periodicity can lead to qualitative changes, such as mode localization, rather than extended Bloch-like waves. The limitations imposed by deviations from perfect periodicity will be carefully characterized for any given analysis, explicitly stating when the Floquet-Bloch framework is used as an approximation.
Computational Efficiency and Scalability: The computational demands of applying Floquet-Bloch analysis, even in its approximate forms, to large-scale neural networks can be substantial. For large networks (many oscillators \(S\)), constructing and analyzing the monodromy matrix for each effective \(\mathbf{q}\) (or graph mode) is demanding. We will investigate and implement the use of iterative Krylov subspace methods (e.g., Arnoldi iteration) for computing dominant Floquet multipliers without explicit matrix formation, significantly enhancing scalability. Further strategies to manage computational costs are discussed in the context of the PhaseScope toolkit (Section 6.3). However, the computational limits for extremely large or highly disordered systems remain an area for ongoing optimization research.
Beyond Simple Stability: The analysis will not be limited to a binary stable/unstable classification. Special attention will be paid to marginal modes (\(|\rho(\mathbf{q})| \approx 1\) or relevant Lyapunov exponents near zero), particularly Goldstone modes (associated with broken continuous symmetries, e.g., translation of a wave) and modes associated with impending bifurcations (e.g., period-doubling where \(\rho(\mathbf{q}) \approx -1\)). Understanding the dynamics of these marginal modes is crucial for predicting pattern selection, slow drifts, and transitions between different spatio-temporal states.
This comprehensive theoretical underpinning, acknowledging both the power of ideal Floquet-Bloch theory and the necessary adaptations for real-world complexities, will enable PhaseScope to provide nuanced insights into the robustness and emergent behavior of collective dynamics in large oscillator arrays.
6.2.4. Theoretical Basis for Active Hidden-Attractor Exploration
The systematic discovery of hidden attractors—formally defined as attractors whose basins of attraction do not intersect with any small neighborhood of an equilibrium point (Leonov & Kuznetsov, 2013; Kuznetsov et al., 2015; see also Section 5.4)—necessitates a departure from purely local analyses or random search. Finding such attractors requires specialized strategies, often involving computational techniques for exploring the state space (e.g., Dudkowski et al., 2016). PhaseScope’s approach to Active Hidden-Attractor Exploration is grounded in a combination of insights from computational geometry, control/perturbation theory, and adaptive learning, applied to the reconstructed state space. We acknowledge that locating _all_ attractors in a high-dimensional, multistable system is generally an NP-hard problem (Pisarchik & Feudel, 2014), and our methods aim for effective heuristic exploration rather than guaranteed completeness. This exploration assumes the capability to reset the network to diverse initial states and apply controlled perturbations. The determination of equilibrium points, while foundational to the strict definition of hidden attractors, can be challenging in complex ONNs; PhaseScope will primarily focus on finding attractors not reachable from typical initializations or known operational states, effectively treating them as operationally hidden.
Embedding-Space Geometry and Topology for Guiding Exploration and Characterizing Discoveries:
The faithfully reconstructed attractor(s) (from Pillar 6.1.1 and Section 6.2.1) and its surrounding embedding space serve as the primary map. We leverage computational geometry and Topological Data Analysis (TDA) techniques, primarily persistent homology (Edelsbrunner & Harer, 2010), to characterize the shape of sampled attractors.
TDA is used here for characterization of trajectories obtained through exploration. For instance, if multiple simulation runs (from varied initial conditions guided by our perturbation strategy) yield trajectories that TDA reveals to possess distinct topological signatures (e.g., different Betti numbers, persistence diagrams), this suggests the discovery of separate, topologically distinct attractors (Yalnız & Budanur, 2020).
Exploration can be guided by identifying “gaps” or low-density regions in the empirically sampled state space (information from EmbedExplorer), or by detecting disconnected components in trajectory data using clustering methods informed by TDA. The boundaries of known basins can be estimated, and exploration biased towards regions outside these known territories, particularly targeting regions of marginal stability identified by SpectraLab (Pillar 6.1.2). While TDA itself doesn’t find hidden attractors, its ability to distinguish complex structures can validate new discoveries and guide further search. We also note the potential of rigorous methods like Conley index theory (e.g., work by Mischaikow et al.) for detecting invariant sets, which could inform future refinements of TopoTrack.
Principled Perturbation Design and Adaptive Learning:
Once potential areas of interest are identified, perturbations must be designed to steer the system towards new basins. Instead of arbitrary noise, PerturbExplorer will employ algorithms that use information from EmbedExplorer (e.g., under-sampled regions) and SpectraLab (e.g., directions of weak stability, eigenvectors of Floquet multipliers near the unit circle, or near-zero Lyapunov exponents) to design targeted perturbations. Such strategies are conceptually related to techniques for attractor switching or targeting unstable orbits (e.g., Ott, Grebogi & Yorke, 1990).
The search for hidden attractors will be framed as an active learning problem (e.g., Ménard et al., 2020). After an initial phase of reconstruction and exploration, the system will adapt its strategy. An information-theoretic criterion will guide the selection of subsequent initial conditions or perturbation parameters. This creates an iterative loop: Explore -> Reconstruct/Analyze (with TDA) -> Identify Knowledge Gaps -> Adaptively Target New Exploration, aiming for efficiency over brute-force methods.
While full formal reachability analysis is often intractable, concepts of local reachability under bounded control can inform perturbation design. The practical application of TDA is also subject to data requirements, which PerturbExplorer will manage through adaptive sampling.
Addressing Scalability and Complementarity to Classical Methods:
The computational cost of exploring high-dimensional state spaces is a significant challenge. PhaseScope will address this through intelligent sampling, dimensionality reduction techniques where appropriate (guided by EmbedExplorer), and by focusing search efforts based on insights from other modules.
Our data-driven exploration is complementary to classical methods like bifurcation analysis and numerical continuation (e.g., using tools like AUTO or MatCont), which systematically track known solutions. PhaseScope’s approach is particularly suited for exploring high-dimensional state spaces where full bifurcation analysis is infeasible or when searching for attractors not easily connected to known solutions.
Statistical Validation of Discovered Regimes:
- Any newly discovered dynamical regime suspected of being a hidden attractor will require rigorous statistical validation to ensure it’s a persistent feature of the system. This involves assessing its stability, estimating its basin size, and ensuring its topological and dynamical distinctness from already known attractors.
By grounding the search in the geometry of the reconstructed state space and employing adaptive, targeted perturbation strategies complemented by TDA-based characterization, PhaseScope aims to provide a more robust and computationally feasible approach to uncovering the full dynamical repertoire of oscillator neural networks. Formalizing these adaptive sampling strategies using frameworks like Bayesian optimization or reinforcement learning represents a promising avenue for future enhancements.
6.3. Toolkit Architecture
To translate the theoretical foundations of PhaseScope into a practical and accessible analytical suite, we propose the development of a modular, integrated software toolkit. This toolkit will provide a coherent, potentially iterative, workflow, guiding users from appropriately formatted oscillator network data (either simulated outputs or experimental recordings, along with a compatible network model definition) through rigorous dynamical analysis to actionable insights.
Implementation Philosophy and Computational Considerations: The PhaseScope toolkit is envisioned to be developed primarily in Python, leveraging its extensive ecosystem of scientific computing, machine learning, and data visualization libraries to ensure broad accessibility and facilitate integration with existing research workflows. A strong emphasis will be placed on creating clear documentation, comprehensive tutorials, and user-friendly interfaces, particularly for the interactive PhaseScope Dashboard (Section 6.3.6). Recognizing the significant computational demands inherent in analyzing large-scale oscillator networks (as highlighted by potential bottlenecks in embedding, Floquet-Bloch analysis, and hidden attractor search), strategies to manage these will be a core design principle. These will include optimized algorithmic implementations, support for parallel processing (CPU/GPU) where feasible, options for different levels of analytical depth or precision to suit various system scales and user needs (e.g., focusing on dominant modes in SpectraLab, or employing heuristic search strategies in PerturbExplorer for initial investigations), and efficient data handling. The architecture is envisioned to comprise the following key modules:
6.3.1. SensorDesigner: Optimal Read-out Placement and Configuration
- Functionality: This module implements the algorithms for optimal sensor selection as outlined in Section 6.2.2. Given a model of the oscillator network (e.g., defined by its governing equations, connectivity, and parameters) or sufficient exploratory data from it, SensorDesigner will identify a minimal or near-optimal set of sensor locations (e.g., specific neurons) or recommend optimal spatial modes (e.g., through data-driven decomposition) for observation.
- Methods: It will incorporate algorithms based on Observability Gramian analysis, potentially including efficient greedy methods, machine learning-driven placement strategies, and tools to assess the observability of different dynamical regimes.
- Output: A recommended sensor configuration (locations/modes) designed to maximize information content for subsequent embedding, along with diagnostics on the expected system observability. This configuration directly informs EmbedExplorer.
6.3.2. EmbedExplorer: Field-Aware Attractor Reconstruction
- Functionality: Responsible for constructing the field-aware delay-coordinate embeddings from the (potentially multi-channel) time-series data, as specified by the “Neural Takens” framework (Section 6.2.1) and configured by SensorDesigner.
- Methods: Supports embeddings from various data types, including direct multi-channel time series and time series of spatial mode coefficients. Includes tools for appropriate preprocessing (e.g., filtering, detrending),
delay time \(tau\) selection (e.g., using advanced mutual information or autocorrelation methods suitable for multi-channel, spatio-temporal data), and embedding dimension \(m\) estimation (e.g., false near-neighbor analysis adapted for field-aware embeddings).
- Output: The reconstructed attractor as a point cloud in the embedding space, associated embedding parameters, and diagnostics of embedding quality. This output is the primary input for SpectraLab, TopoTrack, and the initial state for PerturbExplorer.
6.3.3. SpectraLab: Spatio-Temporal Stability and Spectral Analysis
- Functionality: SpectraLab provides a comprehensive suite of tools for analyzing the spectral properties of network dynamics. Its primary focus is the stability of identified operational modes, utilizing Floquet-Bloch theory for symmetric systems, Lyapunov exponent estimation for general cases, and other advanced spectral methods detailed in Section 6.2.3.
- Methods:
- Floquet/Floquet-Bloch Analysis: Core implementation of Floquet-Bloch theory and its generalizations as detailed in Section 6.2.3. This includes calculating Floquet multipliers/exponents for (spatio-)temporal periodic orbits and leveraging appropriate spectral techniques for networks with varying degrees of structure, from ideal lattices to disordered systems. It will feature efficient numerical methods (e.g., Krylov subspace methods) for scalability.
- Koopman Operator Analysis (Integrated): SpectraLab will also integrate methods for Koopman operator analysis (e.g., DMD and its extensions like EDMD with appropriate dictionaries for spatio-temporal data). This provides a global, linear perspective on the nonlinear dynamics, identifying coherent modes, their growth rates, and frequencies, which complements the local, periodic-orbit-focused stability information from Floquet analysis.
- Output: Quantitative stability characteristics (e.g., Floquet multipliers/exponents, dispersion relations for \(q\), identification of stable/unstable/marginal modes (including Goldstone modes or modes near bifurcation), and dominant Koopman modes, eigenvalues, and eigenfunctions.
6.3.4. TopoTrack: Topological Characterization of State Space
- Functionality: This module employs tools from Topological Data Analysis (TDA) to provide quantitative, coordinate-free characterizations of the reconstructed attractor’s geometry and topology, as well as the broader embedding space.
- Methods: Primarily focused on persistent homology to robustly identify and quantify topological features (connected components, loops, voids, higher-dimensional holes) across different scales from the point cloud data provided by EmbedExplorer. This can also inform the identification of gaps or distinct clusters relevant to PerturbExplorer.
- Output: Persistence diagrams, Betti numbers, and other topological summaries that quantify the shape, complexity, and connectivity of discovered attractors, aiding in their classification and in identifying regions for further exploration.
6.3.5. PerturbExplorer: Active Hidden-Mode Discovery and Basin Mapping
- Functionality: This module implements the strategies for Active Hidden-Attractor Exploration (Sections 6.1.3 and 6.2.4). It enables systematic probing of the network’s state space to discover and map basins of attraction, with a focus on uncovering hidden attractors.
- Methods: It will integrate:
- Algorithms leveraging outputs from EmbedExplorer and TopoTrack to identify promising target regions for exploration (e.g., low-density areas, estimated basin boundaries, topologically distinct zones).
- Tools for designing and applying principled perturbations, potentially guided by stability information from SpectraLab (e.g., perturbing along weakly stable eigendirections).
- Adaptive learning algorithms (as outlined in 6.2.4) to optimize the exploration strategy iteratively, refining the map of attractors and their basins.
- Output: An updated map of discovered attractors (including hidden ones) and their estimated basins, characterizations of newly found dynamical modes, and potentially statistics on inter-attractor transition probabilities. This output can trigger further analysis by other modules.
6.3.6. PhaseScope Dashboard: Integrated Visualization, Diagnostics, and Analysis Hub
- Functionality: The Dashboard serves as the central user interface, providing an interactive environment for orchestrating the analytical workflow, integrating outputs from all modules, and facilitating interpretation.
- Methods: It will offer:
- Advanced, linked visualizations of reconstructed attractors, spatio-temporal network activity, Floquet/Bloch spectra, persistence diagrams, and basin maps.
- Tools for interactive data exploration, parameter adjustment for analyses, and comparative visualization of different network states or models.
- Generation of comprehensive diagnostic summaries and reports.
- Foundation for Future Tuning Guidance: While a full “tuning recommendation” expert system is beyond the initial scope, the Dashboard will be designed to present information (e.g., sensitivity of Floquet exponents to parameters, proximity to bifurcations) in a way that lays the groundwork for future intelligent decision support for network refinement.
- Output: An interactive platform for comprehensive dynamical analysis, reporting, and facilitating an iterative process of discovery and understanding within oscillator-based neural networks.
This modular architecture, emphasizing an iterative analytical workflow (especially between exploration, embedding, and detailed analysis of discovered regimes), is designed for flexibility, robust scientific inquiry, and a pathway towards increasingly automated and insightful understanding of complex oscillatory dynamics.
7. Use Cases & Validation Strategy
To demonstrate PhaseScope’s capabilities and validate its methodologies, we will apply the framework across a spectrum of systems, moving from controlled benchmarks to real-world applications and evaluating performance rigorously.
7.1. Robust Oscillatory Hardware Platforms:
A key application is analyzing and improving emerging hardware (e.g., photonic, neuromorphic VLSI, MEMS, spin-torque oscillators). PhaseScope will be used to identify optimal sensor configurations, assess the stability of computational states under physical nonidealities (noise, drift, fabrication tolerance), and probe for hidden failure modes (parasitic oscillations, undesired locking). The goal is to enable co-design for more robust, reliable real-time phase-encoding hardware, potentially operating near optimal edge-of-chaos regimes.
7.2. Synthetic Benchmarks for Rigorous Validation:
We will test PhaseScope’s core components (embedding, stability analysis, hidden attractor search) on systems with known or analytically tractable dynamics (e.g., forced Kuramoto/van der Pol chains, wave/vortex models). This allows quantitative validation of accuracy and robustness against ground truth, comparative analysis with other tools, and targeted tests like detecting mode collapse.
7.3. Real-World AI Oscillator Network Models:
Applying PhaseScope to contemporary ONN architectures (e.g., harmonic oscillator RNNs for sequences, grid-cell models for spatial cognition, simulated neuromorphic circuits) is crucial for demonstrating practical utility. We will characterize operational manifolds, assess functional state stability, and search for hidden failure modes to understand performance limitations and guide the design of more robust and predictable AI models.
7.4. Evaluation Metrics:
Success will be measured using tailored quantitative and qualitative metrics:
- Embedding Fidelity: Comparing reconstructed attractor invariants (dimensions, topology) to known values (e.g., target <5% error for benchmark fractal dimensions); embedding continuity statistics.
- Stability Accuracy: Comparing computed Lyapunov/Floquet spectra against known values or direct simulations (e.g., target <2% error for dominant Floquet multipliers in benchmarks); matching predicted bifurcations.
- Hidden Mode Discovery: Measuring success rate and efficiency in finding known hidden attractors in benchmarks (e.g., target >95% detection with
- Edge-of-Chaos Indicators: Monitoring Lyapunov exponents near zero, Floquet multipliers near unity, and topological shifts to flag critical boundaries.
- Performance & Usability: Assessing algorithmic scalability and gathering user feedback on the toolkit’s usability and interpretability.
By applying PhaseScope across these cases and using rigorous metrics, we aim to demonstrate its transformative potential for analyzing and designing oscillator-based AI.
8. Roadmap & Milestones
The PhaseScope project will follow a phased development approach, balancing theory, implementation, and validation.
- Phase I: Foundational Theory & Core Algorithms. Establish theoretical underpinnings ("Neural Takens” conditions, sensor placement) and develop initial prototypes of SensorDesigner, EmbedExplorer, and basic SpectraLab (Floquet analysis).
- Phase II: Prototyping & PDE Validation. Create a functional core toolkit prototype and validate embedding and spectral analysis on benchmark PDEs (e.g., Kuramoto-Sivashinsky). Develop initial PerturbExplorer and integrate core modules into a command-line workflow. Publish initial theoretical results.
- Phase III: Advanced Features & Dashboard. Integrate advanced methods (Koopman, TDA) into SpectraLab and TopoTrack. Fully develop PerturbExplorer with adaptive strategies. Create the interactive PhaseScope Dashboard (v1.0 Beta). Apply the toolkit to a complex simulated ONN and implement edge-of-chaos monitoring.
- Phase IV: Case Studies, Release & Hardware Validation. Demonstrate broad utility via diverse ONN case studies and publications. Release the PhaseScope toolkit open-source with documentation and tutorials. Validate on physical oscillator hardware data (e.g., photonic, neuromorphic) via collaborations. Develop educational materials and explore extensions like automated tuning.
9. Frontier Challenges & Open Questions
PhaseScope engages with several key frontiers in the analysis of complex systems, opening avenues for future research:
- 9.1. Minimal Sensor Sets for Embedding: Determining the minimal sensor configuration for guaranteed embedding in complex, noisy ONNs remains challenging. Future work includes developing adaptive sensor strategies, integrating compressed sensing principles, and understanding fundamental observability limits.
- 9.2. Operator-Theoretic Control of Attractor Landscapes: Moving beyond single-state stabilization, a frontier is using operator theory (e.g., Koopman) to control the entire attractor landscape—shaping basins, managing hidden attractors, and guiding transitions—potentially enabling a “spectral theory of control” or a “dynamical grammar.”
- 9.3. Topology-Aware Training and Design: Incorporating topological insights (TDA) directly into ONN training is a key challenge, involving topology-aware loss functions, understanding architecture-topology links, and using topological fingerprints.
- 9.4. Robustness to Real-World Constraints: Ensuring robustness under hardware constraints (noise, quantization, real-time demands) requires understanding noise effects on stability (potentially via stochastic extensions), analyzing quantization impacts, adapting diagnostics for online use, and defining principles for graceful degradation.
- 9.5. Interpreting High-Dimensional Dynamics: Functionally interpreting complex, high-dimensional embeddings and linking geometry to computation remains a significant hurdle requiring new abstractions and visualization tools.
- 9.6. Non-Stationary Dynamics: Adapting analysis tools to non-stationary dynamics (e.g., during training or adaptation) involves developing methods for time-varying embeddings, generalizing stability concepts, and tracking transient attractors.
- 9.7. Integration with Differentiable Frameworks: Integrating PhaseScope’s diagnostics into differentiable programming frameworks (e.g., JAX, PyTorch) could enable direct optimization for dynamical properties, requiring differentiable algorithms and new loss function formulations.
Addressing these challenges will advance PhaseScope and contribute broadly to dynamical systems, AI, computational neuroscience, and physics-informed machine learning.
10. Call to Action & Collaboration
The PhaseScope project is an ambitious endeavor to transform the analysis and design of oscillator-based AI systems. Its success and impact will be significantly amplified through collaborative efforts. We are actively seeking to engage with researchers, engineers, and domain experts who share our vision and can contribute to the development and application of the PhaseScope framework and toolkit.
We are particularly interested in collaborations with:
- Theoretical Dynamists & Mathematicians: To advance the rigorous mathematical underpinnings of PhaseScope (e.g., “Neural Takens” theorem, Floquet-Bloch theory for complex systems).
- Computational Scientists & Software Engineers: To contribute to building a robust, scalable, and user-friendly PhaseScope toolkit.
- AI Researchers & Machine Learning Practitioners: To partner in applying PhaseScope to cutting-edge oscillator neural networks and neuromorphic systems, helping to test its capabilities and provide valuable feedback as the toolkit matures.
- Domain Experts & Experimentalists (e.g., Photonics, Neuroscience, Robotics): To collaborate on applying and validating PhaseScope with real-world data from physical oscillator systems, providing crucial testbeds for its methodologies.
If your expertise aligns with these areas and you are interested in contributing to or exploring future applications with PhaseScope, please reach out: s@samim.ai.
11. Conclusion
Oscillator-based neural networks (ONNs) offer novel AI paradigms but remain hindered by their complex, often opaque internal dynamics, leading to challenges in robustness and reliability. The PhaseScope framework directly addresses this by integrating Field-Aware Embedding Theory, Spectral Stability Diagnostics, and Active Hidden-Attractor Exploration into a unified “microscope” for these systems. This approach moves beyond heuristics towards stronger theoretical foundations and principled analytical tools, aiming to make the analysis, design, and deployment of ONNs more rigorous and trustworthy.
By providing an accessible toolkit (the PhaseScope Toolkit) to characterize dynamics, assess stability, and uncover hidden operational modes, PhaseScope endeavors to enable more robust and interpretable oscillatory AI. While significant challenges and open questions remain (Section 9), this project represents a commitment to fostering a deeper understanding of complex AI systems. Realizing this vision requires collaboration (Section 10), and we invite engagement from researchers and engineers interested in advancing the next generation of intelligent technologies built on coupled oscillators.

12. References
- Coifman, R. R., & Lafon, S. (2006). Diffusion maps. _Applied and Computational Harmonic Analysis_, 21(1), 5–30.
- Edelsbrunner, H., & Harer, J. (2010). _Computational Topology: An Introduction_. American Mathematical Society.
- Golubitsky, M., & Stewart, I. (2002). _The Symmetry Perspective: From Equilibrium to Chaos in Phase Space and Physical Space_. Birkhäuser.
- Jones, D. R., Schonlau, M., & Welch, W. J. (1998). Efficient global optimization of expensive black-box functions. _Journal of Global Optimization_, 21(4), 345–361.
- Kuramoto, Y. (1984). _Chemical Oscillations, Waves, and Turbulence_. Springer.
- Kuramoto, Y., & Tsuzuki, T. (1976). Persistent propagation of concentration waves in dissipative media far from thermal equilibrium. _Progress of Theoretical Physics_, 55(2), 356–369.
- Kuznetsov, N. V., Leonov, G. A., & Mokaev, T. N. (2015). Hidden attractors in fundamental problems and engineering models. _arXiv:1510.04803_.
- Leonov, G. A., & Kuznetsov, N. V. (2013). Hidden attractors in dynamical systems. From hidden oscillations in Hilbert–Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractors in Chua circuits. _International Journal of Bifurcation and Chaos_, 23(1), 1330002.
- Mezić, I. (2005). Spectral properties of dynamical systems, model reduction and decompositions. _Nonlinear Dynamics_, 41, 309–325.
- Nayfeh, A. H., & Balachandran, B. (1995). _Applied Nonlinear Dynamics: Analytical, Computational, and Experimental Methods_. Wiley, Ch. 7.
- Rabinowitz, P. H. (2000). _Methods of Nonlinear Analysis: Applications to ODEs and Variational Problems_. Birkhäuser, Sec. 8.4.
- Rakshit, S., Bera, B. K., Perc, M., & Ghosh, D. (2017). Basin stability for chimera states. _Scientific Reports_, _7_, 2412.
- Rezounenko, A. V. (2003). Approximate inertial manifolds for retarded semilinear parabolic equations. _Journal of Mathematical Analysis and Applications_, 282(2), 614–630.
- Robinson, J. C. (2005). A topological delay embedding theorem for infinite-dimensional dynamical systems. _Nonlinearity_, 18(5), 2135–2143.
- Sauer, T., Yorke, J. A., & Casdagli, M. (1991). Embedology. _Journal of Statistical Physics_, 65(3–4), 579–616.
- Schmid, P. J. (2010). Dynamic mode decomposition of numerical and experimental data. _Journal of Fluid Mechanics_, 656, 5–28.
- Takens, F. (1981). Detecting strange attractors in turbulence. In _Dynamical Systems and Turbulence, Warwick 1980_, Lecture Notes in Mathematics, vol. 898, pp. 366–381. Springer.
- Temam, R. (1997). _Infinite-Dimensional Dynamical Systems in Mechanics and Physics_, 2nd ed. Springer.
- Theiler, J. (1990). Estimating fractal dimension. _Journal of the Optical Society of America A_, 7(6), 1055–1073.
- van der Pol, B. (1926). On relaxation-oscillations. _Philosophical Magazine_, 2, 978–992.
- Wolf, A., Swift, J. B., Swinney, H. L., & Vastano, J. A. (1985). Determining Lyapunov exponents from a time series. _Physica D_, 16(3), 285–317.
- Stark, H., et al. (2003). Embedding delay coordinates: A method for analyzing deterministic systems. _Physica D_, 180(3-4), 153–192.
- Panaggio, M., & Abrams, D. M. (2015). Chimera states: Coexistence of coherence and incoherence in dynamical networks. _Proceedings of the National Academy of Sciences_, 112(48), 14837–14842.
- Brunton, S. W., et al. (2016). Koopman invariant subspaces for learning nonlinear dynamical systems. _arXiv:1611.03534_.
- Kukavica, I., & Robinson, J. C. (2004). Distinguishing smooth functions by a finite number of point values, and applications to the embedding of attractors. _Physica D: Nonlinear Phenomena_, 198(3-4), 215-225.
- Whitney, H. (1936). Differentiable manifolds. _Annals of Mathematics_, 37(3), 645–680.
- Barahona, M., & Pecora, L. M. (2002). Synchronization in small-world networks. _Physical Review Letters_, 88(5), 054101.
- Pecora, L. M., & Carroll, T. L. (1998). Master stability functions for synchronized coupled systems. _Physical Review Letters_, 80(10), 2109–2112.
- Ott, E., Grebogi, C., & Yorke, J. A. (1990). Controlling chaos. _Physical Review Letters_, 64(11), 1196–1199.
- Pisarchik, A. N., & Feudel, U. (2014). Control of multistability. _Physics Reports_, 540(4), 167–218.
- Yalnız, G., & Budanur, N. B. (2020). Topological similarity of chaotic attractors and periodic orbits. _Chaos: An Interdisciplinary Journal of Nonlinear Science_, 30(8), 083101.
- Strogatz, S. H. (2000). _Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering_. Perseus Books. (Or a more specific paper if intended for disordered systems)
- Bertschinger, N., & Natschläger, T. (2004). Real-time computation at the edge of chaos in recurrent neural networks. _Neural Computation_, 16(7), 1413–1436.
- Lehoucq, R. B., Sorensen, D. C., & Yang, C. (1998). _ARPACK Users’ Guide: Solution of Large-Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods_. SIAM.
- Guillemin, V., & Pollack, A. (1974). _Differential Topology_. Prentice-Hall.
- Kailath, T. (1980). _Linear Systems_. Prentice-Hall.
- Roy, K. (2019). Spintronic devices for neuromorphic computing. _Journal of Physics D: Applied Physics_, 52(2).
- Cao, L. (1997). Practical method for determining the minimum embedding dimension of a scalar time series. _Physica D: Nonlinear Phenomena_, 110(1-2), 43–50.
- Dudkowski, D., Jafari, S., Kapitaniak, T., Kuznetsov, N. V., Leonov, G. A., & Prasad, A. (2016). Hidden attractors in dynamical systems. _Physics Reports_, _637_, 1-50.
- Ménard, P., Domingues, O. D., Jonsson, A., Kaufmann, E., Leurent, E., & Valko, M. (2020). Fast active learning for pure exploration in reinforcement learning. _arXiv preprint arXiv:2007.13442_.
Appendix A: Glossary
- Attractor: A set of states in a dynamical system towards which the system evolves over time from a given set of initial conditions within its basin of attraction.
- Basin of Attraction: The set of initial conditions in the state space of a dynamical system that will lead trajectories to converge to a particular attractor.
- Bifurcation: A qualitative change in the dynamical behavior of a system (e.g., creation or destruction of attractors, or a change in their stability) as a system parameter is varied.
- Bloch’s Theorem/Mode: In spatially periodic systems (like crystal lattices or regular oscillator arrays), Bloch’s theorem states that solutions to certain linear differential equations (like the Schrödinger equation or equations governing wave propagation) take the form of a plane wave modulated by a function with the same periodicity as the underlying system. These solutions are called Bloch modes or Bloch waves. It is a key concept for understanding wave propagation in periodic media and forms the basis for Floquet-Bloch analysis in spatially extended systems.
- Box-Counting Dimension: A method of determining the fractal dimension of a set in a metric space by measuring how the number of boxes of a given size needed to cover the set scales as the box size decreases. It is often used to characterize the complexity of strange attractors.
- Chimera States: Complex spatio-temporal patterns in networks of coupled oscillators where domains of synchronized (coherent) and desynchronized (incoherent) behavior coexist.
- Delay-Coordinate Embedding: A technique used to reconstruct a representation of a dynamical system’s state space (attractor) from a single time series of observations. It involves creating vectors whose components are time-delayed values of the observed time series. The theoretical basis for this is Takens’ Theorem and its extensions.
- Dynamic Mode Decomposition (DMD): A data-driven dimensionality reduction and system identification technique, often associated with Koopman operator analysis, that extracts coherent spatio-temporal modes and their corresponding temporal dynamics from complex data.
- Edge-of-Chaos: A critical dynamical regime, often considered computationally rich, where a system operates near the boundary between ordered (e.g., periodic or stable) and chaotic behavior.
- Embedding Dimension \(m\): In the context of delay-coordinate embedding, this is the number of delayed coordinates used to construct each state vector in the reconstructed phase space. Choosing an appropriate \(m\) is crucial for a faithful embedding.
- Field-Aware Embedding: A theoretical approach, central to PhaseScope, for reconstructing the state space of spatially distributed oscillator networks from multi-channel sensor data, explicitly accounting for the field-like nature of the observations.
- Floquet Theory/Multipliers/Exponents: Floquet theory is a branch of mathematics dealing with the stability of solutions to linear ordinary differential equations with time-periodic coefficients. It analyzes the behavior of solutions over one period. Floquet multipliers are characteristic values (eigenvalues of the monodromy matrix) associated with the system over one period; their magnitudes determine the stability of a periodic orbit (e.g., if all multipliers are within the unit circle in the complex plane, the orbit is stable). Floquet exponents are the logarithms of these multipliers and relate to the average rate of divergence or convergence of nearby trajectories.
- Hidden Attractor: An attractor in a dynamical system whose basin of attraction does not intersect with any small neighborhood of an equilibrium point. This means it cannot be found by starting simulations from initial conditions close to equilibria, requiring specialized search techniques.
- Inertial Manifold: For many infinite-dimensional dissipative dynamical systems (like those described by certain PDEs), an inertial manifold is a finite-dimensional, positively invariant, exponentially attracting manifold that captures the long-term dynamics of the system. The dynamics on this manifold are governed by a finite set of ordinary differential equations called an inertial form. Its existence implies that the essential dynamics, however complex, are fundamentally finite-dimensional.
- Koopman Operator: An infinite-dimensional linear operator that governs the evolution of all possible (scalar) observable functions of the state of an autonomous dynamical system. It provides a powerful alternative, linear representation of nonlinear dynamics in the space of observables, whose eigenfunctions and eigenvalues reveal important dynamical modes and frequencies.
- Limit Cycle: A type of attractor in a dynamical system that corresponds to an isolated, stable periodic trajectory.
- Lyapunov Exponents: A set of values that quantify the average exponential rate of divergence or convergence of nearby trajectories in the state space of a dynamical system. A positive maximal Lyapunov exponent is a hallmark of chaos.
- Master Stability Function (MSF): A method used to determine the stability of synchronized states in networks of coupled identical oscillators by analyzing the eigenvalues of the network’s coupling matrix in conjunction with the variational equation of an individual oscillator.
- Neural Takens Theorem: A conjectured extension of classical embedding theorems, proposed by PhaseScope, aiming to provide rigorous conditions under which the dynamics of spatially distributed oscillator neural networks can be faithfully reconstructed from a finite set of multi-channel observations.
- Observability Gramian: A matrix used in control theory for linear systems to determine whether the internal states of the system can be inferred from its outputs over a given time interval. It quantifies how well states can be observed from a given set of sensors; a non-singular Gramian implies observability. Its properties are used in optimal sensor placement.
- Oscillator-based Neural Networks (ONNs): Computational models inspired by neurobiological systems that use the collective dynamics of coupled oscillators, often leveraging phase-encoding, to perform information processing tasks.
- Persistent Homology: A tool from Topological Data Analysis (TDA) that identifies and tracks topological features (such as connected components, loops, voids) of a point cloud or simplicial complex across a range of scales. It helps distinguish robust, significant features from noise by observing how long they “persist” as the scale parameter changes.
- Phase-Encoding: A method of representing information where the phase of an oscillator (or the relative phases between multiple oscillators) encodes the relevant data or computational state.
- Spatio-temporal Pattern: A pattern or structure that exhibits organization in both space and time, such as traveling waves, spiral waves, synchronized domains, or chimera states in a spatially extended system.
- State Space: The abstract multi-dimensional space in which every possible state of a dynamical system is represented by a unique point. The evolution of the system corresponds to a trajectory in this space.
- Takens’ Theorem: A fundamental result in dynamical systems theory which states that, under certain genericity conditions (on the system dynamics and the observation function), a delay-coordinate embedding of a time series from a compact attractor can faithfully reconstruct the topology of that attractor, provided the embedding dimension is sufficiently large (typically \(m\), where \(d_A\) is the dimension of the attractor). It justifies using time-delayed measurements from a single sensor to understand multi-dimensional dynamics.
- Genericity (in dynamical systems): A property is said to be generic if it holds for a “typical” system or observation within a given class, specifically for all elements in an open and dense subset of the space of systems or functions. In embedding theory, for example, Takens’ theorem requires a generic observation function.
- Krylov Subspace Methods: A class of iterative numerical algorithms used primarily for solving large, sparse linear systems of equations or for finding eigenvalues and eigenvectors of large matrices. Methods like Arnoldi iteration, used in PhaseScope for computing dominant Floquet multipliers, fall into this category, offering computational efficiency by working within a smaller “Krylov subspace” rather than with the full matrix.
- Observability: A property of a dynamical system indicating whether its internal states can be uniquely determined from knowledge of its external outputs over a period of time. In PhaseScope, achieving spatio-temporal observability is crucial for faithfully reconstructing attractor dynamics from sensor measurements.
- Spectral Analysis (in dynamical systems): A broad set of techniques used to study the behavior and stability of dynamical systems by analyzing the eigenvalues and eigenfunctions (or modes) of operators associated with the system’s evolution. Examples include Floquet theory (for periodic systems), Koopman operator analysis (for a linear perspective on nonlinear dynamics), and Lyapunov exponent calculation (for chaotic systems).
- Topological Data Analysis (TDA): A field that applies tools from algebraic topology to analyze and understand the “shape” (e.g., connectivity, holes, voids) of complex, often high-dimensional, datasets. Persistent homology, a key technique in TDA and used in PhaseScope’s TopoTrack module, helps identify robust topological features at different scales.