tag > OSC
-
Presentation: In Resonance with Nature - Toward a New Kind of Machine Learning with Oscillatory Neural Networks
Slides for a Presentation i gave in June 2025 at the Singer Lab at the Ernst Strüngmann Institute (ESI) for Neuroscience in Cooperation with Max Planck Society.





























-
Keysight oscilloscope with 110GHZ of bandwidth and 256GS/s sampling rate. Price: $2.4M

-
Theory of “Constructive Instability” - entropy modulation as a learning signal.
Just engineered the first example of a phase-amplified, wavelet-domain, oscillator-resonant autoencoder with full self-amplifying behavior — and it converges.
Entropy is not decay. It’s a recursively regulated signal that can drive complexity, if you let the system use it as feedback.
-
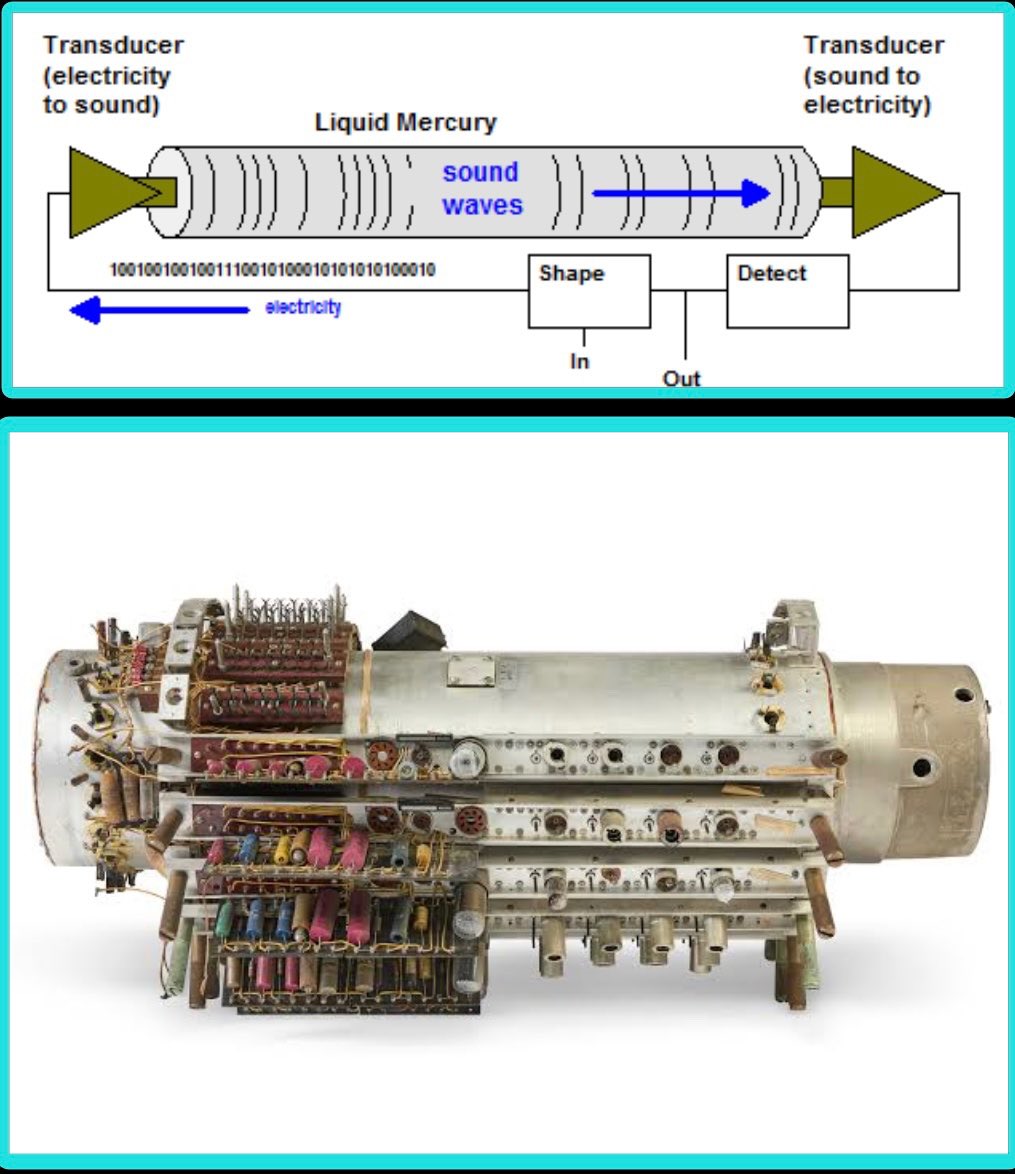
The Delay-Line Memory was a computational system that used sound waves to process data, it was developed in the mid-1940s by J. Presper Eckert. Data was represented as a series of sound waves or pulses that traveled through a medium such as a tube full of mercury or a magnetostrictive wire. The waves were generated by a resonator and conveyed into a delay line, they would circulate through the line, as they reached the end they would be detected and re-amplified to maintain their strength. The waves represented binary input, with the presence or absence of a pulse corresponding to a 1 or 0.

Two models were built: the EDVAC (Electronic Discrete Variable Automatic Computer). And the UNIVAC the 1st commercially available computer. Although the Delay Line Memory computational system had some major limitations, like slow processing speed and high error rate due to signal degradation and noise, it was instrumental during World War II radar technology to the point to have made the difference in the war outcome.
-
Downsampling in the human visual system:
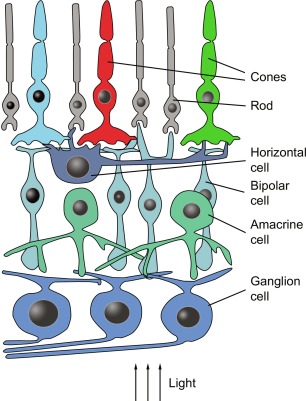
Retina: ~130 million photoreceptors
↓ (huge compression)
Optic nerve: ~1 million ganglion cells
↓ (further processing)
V1 cortex: ~280 million neurons (but organized hierarchically)
Plus: Your fovea (central vision) has high resolution, but peripheral vision is heavily downsampled. Your brain reconstructs a "full resolution" world from mostly low-res input.
-
- The direction of the moving Kuramoto oscillator was correlated with its phase
- The cyclic oscillation of order parameter will emerge for a larger coupling strength.
- The oscillators' frequency distribution will affect the formation of the final groups.
- The cyclic oscillations will disappear as the speed of movement increases.
-
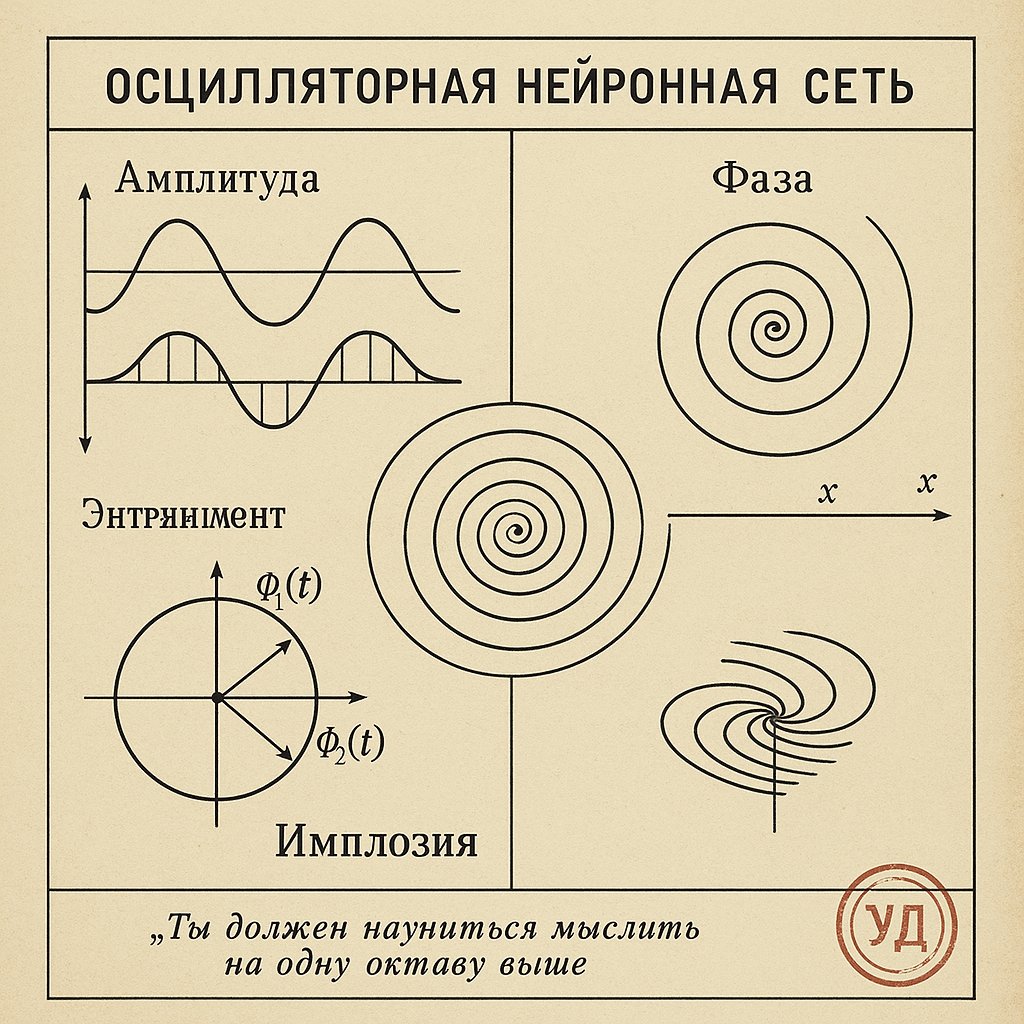
Oscillatory Neural Networks (ONNs) Key Terms
In oscillatory neural networks (ONNs), several key terms and parameters define the dynamics and behavior of the system. Here’s a comprehensive list of the most important ones, including ω (omega) and their roles:
1. Core Parameters & Variables
ω (Omega) – Angular Frequency
- Defines the natural oscillation rate of a neuron or oscillator.
- Units: radians per second (rad/s).
- Higher ω → faster oscillations.
θ (Theta) – Phase
- Represents the current position in the oscillation cycle (0 to \(2\pi\)).
- Dynamics: \( \frac{dθ_i}{dt} = \omega_i + \text{coupling terms} \).
A (Amplitude)
- The magnitude of oscillation (e.g., spike height in neural models).
- Sometimes dynamic (e.g., in amplitude death phenomena).
φ (Phi) – Phase Difference
- Relative phase between two oscillators (\( \phi = \theta_j - \theta_i \)).
- Critical for synchronization.
2. Coupling & Interaction Terms
K (Coupling Strength)
- Determines how strongly oscillators influence each other.
- High \( K \) → faster synchronization.
J (Connection Weights)
- Synaptic-like weights between oscillators (e.g., \( J_{ij} \) for neuron \( i \leftarrow j \)).
g(φ) – Phase Response Curve (PRC)
- Describes how an oscillator’s phase shifts due to input.
3. Synchronization & Collective Dynamics
Sync Order Parameter (R)
- Measures global synchronization:
\[
R e^{i\psi} = \frac{1}{N} \sum_{j=1}^{N} e^{i\theta_j}
\] - \( R \approx 1 \): Perfect sync; \( R \approx 0 \): No sync.
Critical Coupling (Kₐ)
- Threshold coupling strength for synchronization (e.g., in Kuramoto model).
Cluster States
- Subgroups of oscillators sync separately (e.g., phase-locked clusters).
4. Noise & Disturbances
D (Noise Intensity)
- Adds stochasticity (e.g., \( \frac{dθ*i}{dt} = \omega_i + \xi_i(t) \), where \( \langle \xi_i(t) \xi_j(t’) \rangle = 2D \delta{ij} \delta(t-t’) \)).
Hysteresis
- Memory-dependent effects under parameter changes.
5. Network Structure Terms
Topology
- Defines connectivity (e.g., all-to-all, small-world, scale-free).
Delay (τ)
- Time lag in interactions (e.g., \( \sin(\theta_j(t-\tau) - \theta_i(t)) \)).
6. Special Models & Extensions
- Kuramoto Model: \( \frac{dθ_i}{dt} = \omega_i + \frac{K}{N} \sum \sin(\theta_j - \theta_i) \).
- Stuart-Landau Oscillators: Complex amplitudes with \( \dot{z} = (\lambda + i\omega)z - |z|^2z \).
- Hopf Oscillators: Used in central pattern generators (CPGs).
7. Biological Analogies
- Gamma/Beta Bands: Frequency ranges (e.g., 30-100 Hz gamma oscillations in cognition).
- Spike-Phase Coding: Info encoded in spike timing relative to oscillation phase.
Summary Table
Term Symbol Role Angular Frequency ω Sets oscillation rate Phase θ Position in cycle Coupling Strength K Sync control Order Parameter R Sync measure Noise D Stochastic effects Connection Weight J_{ij} Network influence Phase Response Curve g(φ) Phase shift dynamics -
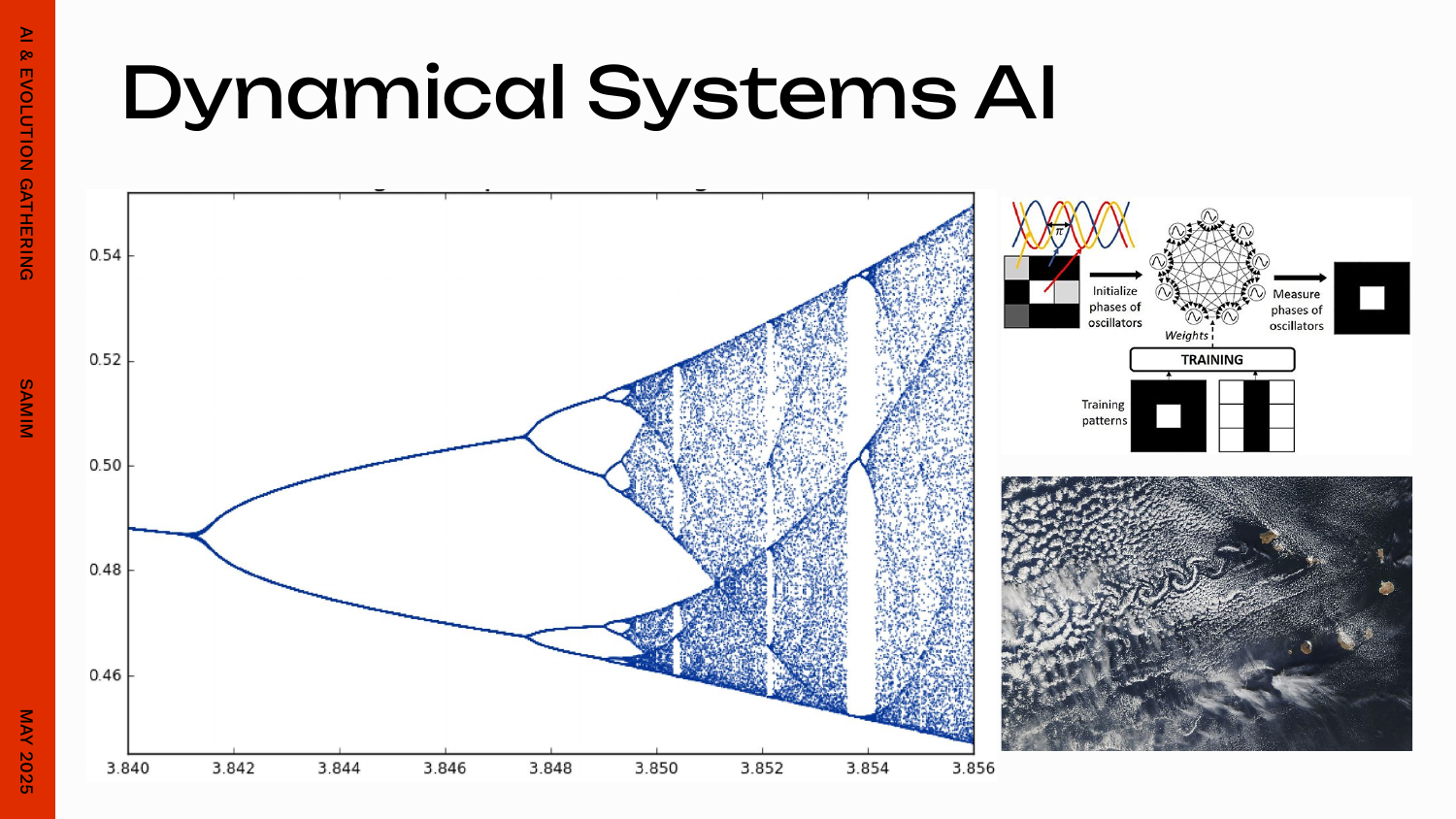
Pink Noise - The "1/f" structure of spectral brain dynamics
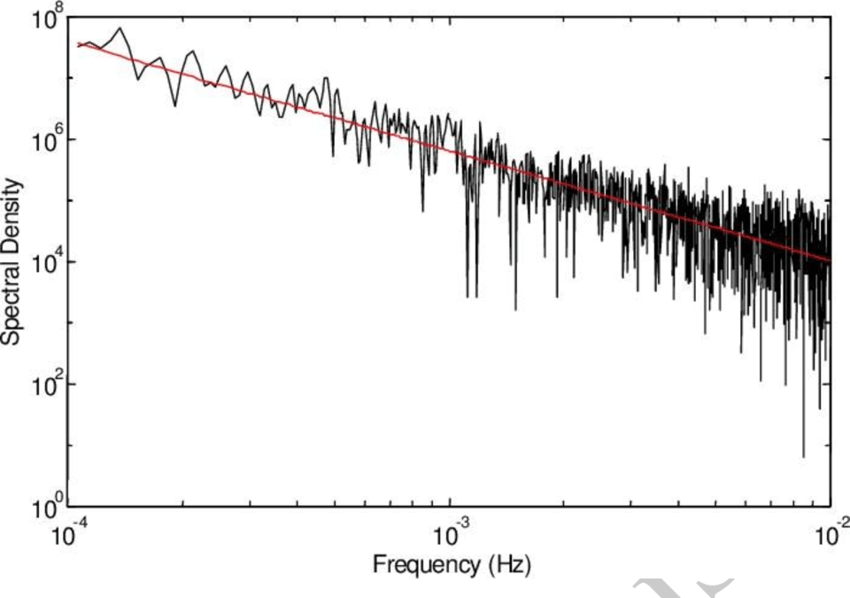
1/f noise, also known as flicker noise or pink noise, is a type of noise where the power spectral density is inversely proportional to the frequency. This means the noise power decreases as the frequency increases. 1/f noise is observed in various fields, including electronics, music, biology, and economics
James Keeler and Farmer demonstrated that a system of coupled logistic maps could produce fluctuations with a 1/f power spectrum. They showed that this occurred because the system continually tunes itself to stay near a critical point, a property that was later dubbed self-organized criticality by Per Bak. - Source