Synchronized Oscillators (via)
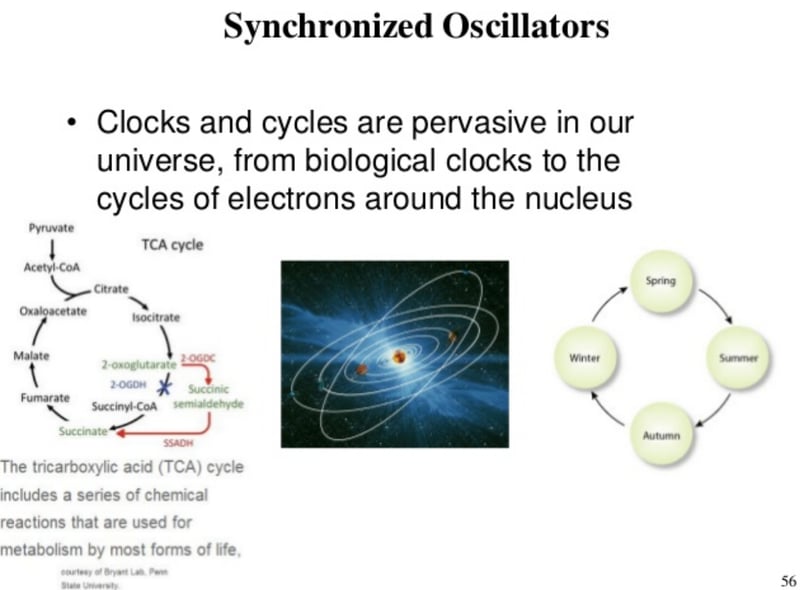

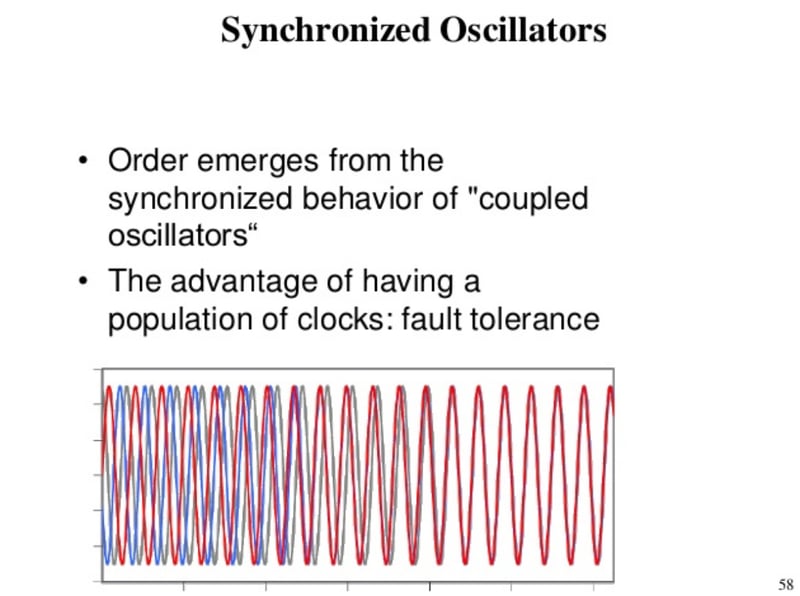



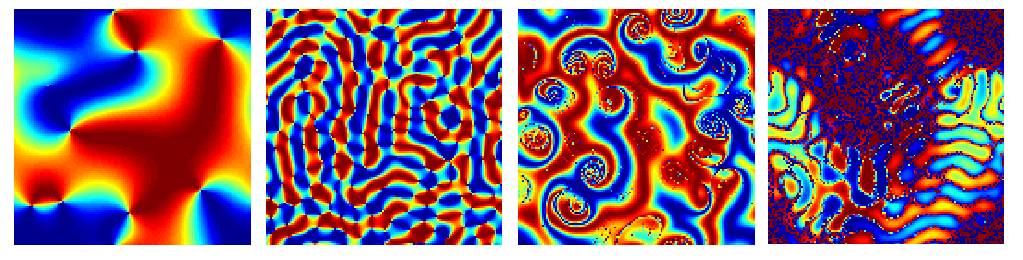
In 1975, Yoshiki Kuramoto introduced a simple model to describe the collective dynamics of a set of interacting oscillators. In the model, each oscillator has a natural frequency, and is coupled equally to all other oscillators. Assuming a fixed spread in oscillator frequencies, Kuramoto showed that in the limit of a large number of oscillators, the model exhibits a continuous phase transition from asynchronous to synchronous behaviour with increasing inter-oscillator coupling. Since then, the model and generalizations of it have been widely used in exploring the synchronization behavior in groups of biological cells, fireflies, superconducting Josephson junctions, or the movements of swarms or flocks of organisms.
- Yoshiki Kuramoto: https://en.wikipedia.org/wiki/Yoshiki_Kuramoto
- Kuramoto model: https://en.wikipedia.org/wiki/Kuramoto_model
- Kuramoto Model of Synchronized Oscillators https://blogs.mathworks.com/cleve/2019/08/26/kuramoto-model-of-synchronized-oscillators/
- All together now https://www.nature.com/articles/421780a
- pyclustring: https://github.com/annoviko/pyclustering
- Continuous vs. Discontinuous Transitions in the D-Dimensional Generalized Kuramoto Model: https://arxiv.org/pdf/1806.01314.pdf
- Synchronization networks https://en.wikipedia.org/wiki/Synchronization_networks
- Oscillatory neural network: https://en.wikipedia.org/wiki/Oscillatory_neural_network
- Synchronization: https://en.wikipedia.org/wiki/Synchronization
- An Oscillatory Neural Autoencoder Based on Frequency Modulation and Multiplexing: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6048285/
- A Neural Network Based on Synchronized Pairs of Nano-Oscillators https://arxiv.org/abs/1709.02274v1
Image: Synchronization patterns in a two-dimensional array of Kuramoto-like oscillators