tag > FFHCI
-
Extend your senses and be amazed: My surveillance cameras with AI anomaly detection are paying off. Caught a meteor on camera last night.

My surveillance cameras with AI anomaly detection flagged this at 2:37 AM last night. It couldn’t classify it. What is it?

"Extend your senses and be amazed." That’s the theme of this experiment—turning cheap cameras and off-the-shelf ML models into a DIY surveillance network. The barrier to entry? Lower than ever. The possibilities? Endless. Want to see how it’s done? 👀
-
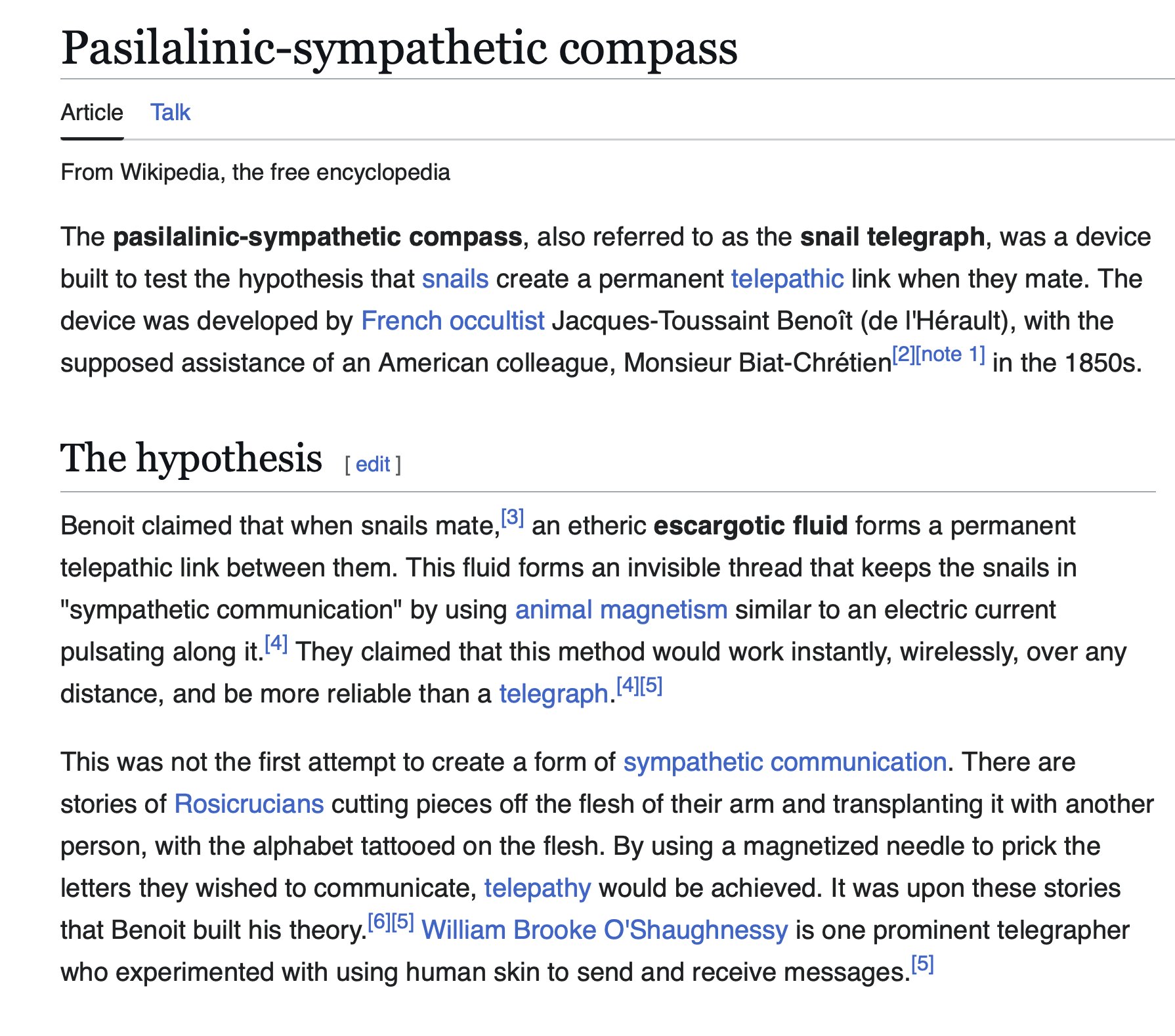
"Recent research into plant perception and communication has provided new surprising details into the life of plants enjoying not only ability of communication through chemical volatiles but also perception of acoustic signals. Moreover, research done on the visual capabilities of algae and protists clearly suggest vision already in unicellular organisms. Experimental testing of the ocelli-based plant vision, as it was done by Harold Wager, would be the logical next step in our quest for understanding the plant sensory complexity."


-
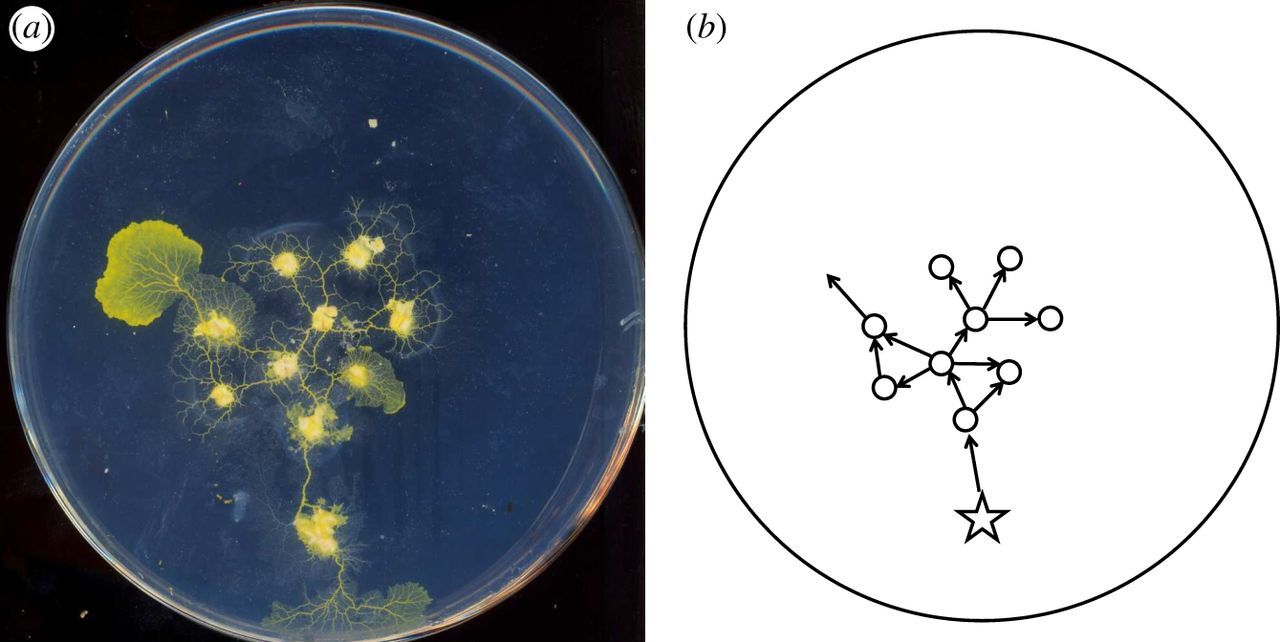
In the world of Slime Mold Computing, @AAdamatzky was ahead of his time with papers like "Slime mould processors, logic gates and sensors" (2015). Molds excel at highly parallel, non-deterministic tasks.
-
Talk is cheap: rediscovering sounds made by plants
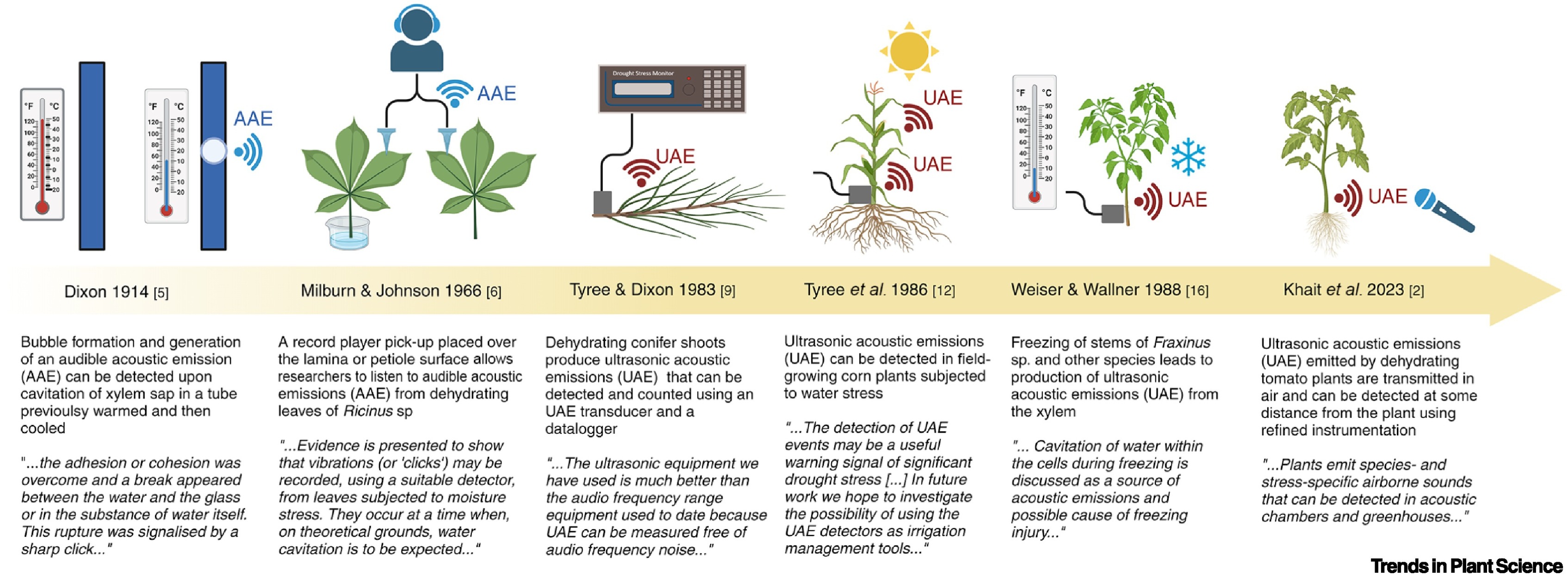
Recent reports of airborne sound emissions by plants under drought stress have generated interest, leading to speculative ideas on plant–animal and plant–plant communication.
Research on sound production by plants is more than 100 years old, with John Milburn demonstrating in 1966 that these sounds are mainly produced by xylem cavitation events and can be detected with dedicated instruments.
Research from 1970 onward has shown that sounds can also be produced by other passive physical processes in plants, and also demonstrated that acoustic emissions can be used to monitor the water status of plants in the field.
The hypothesis that sounds produced by plants are informative for insects feeding on stressed plants, or even for neighboring plants, is attractive but still purely speculative to date.
-
Prediction: One of the most impressive outcomes of multimodal AI models becoming easy to train and use will be its contributions to interspecies communication and collaboration.
-
Tree stump and human fingerprint

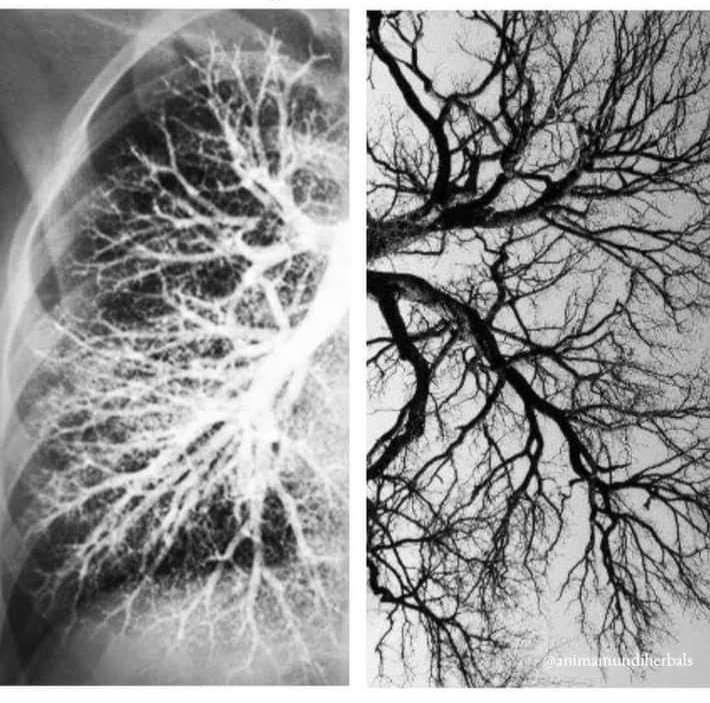
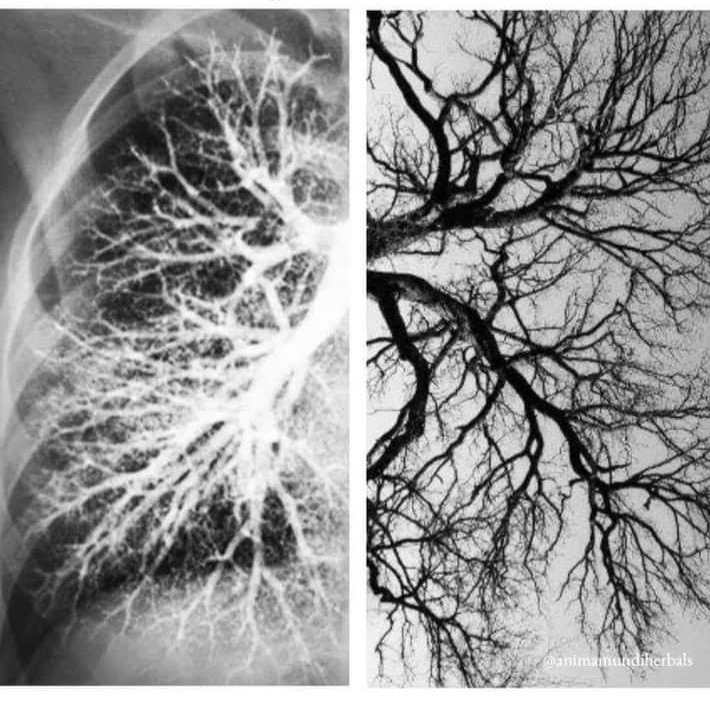
Human lungs and tree branches
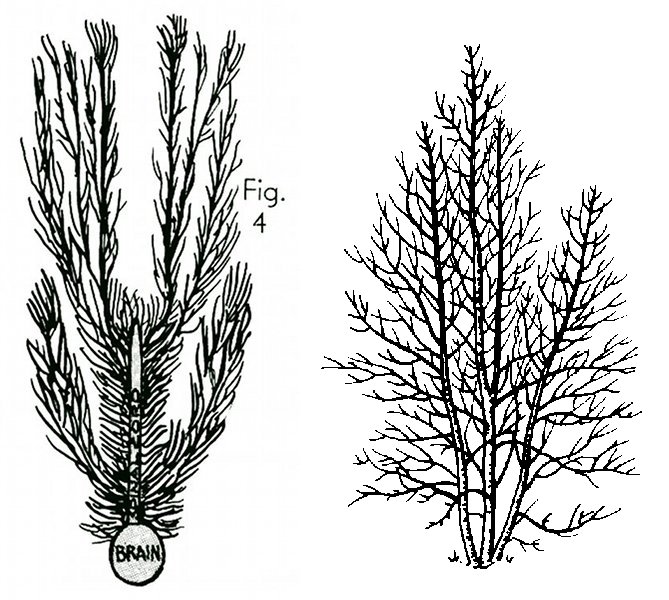
Human nervous system and Tree branches
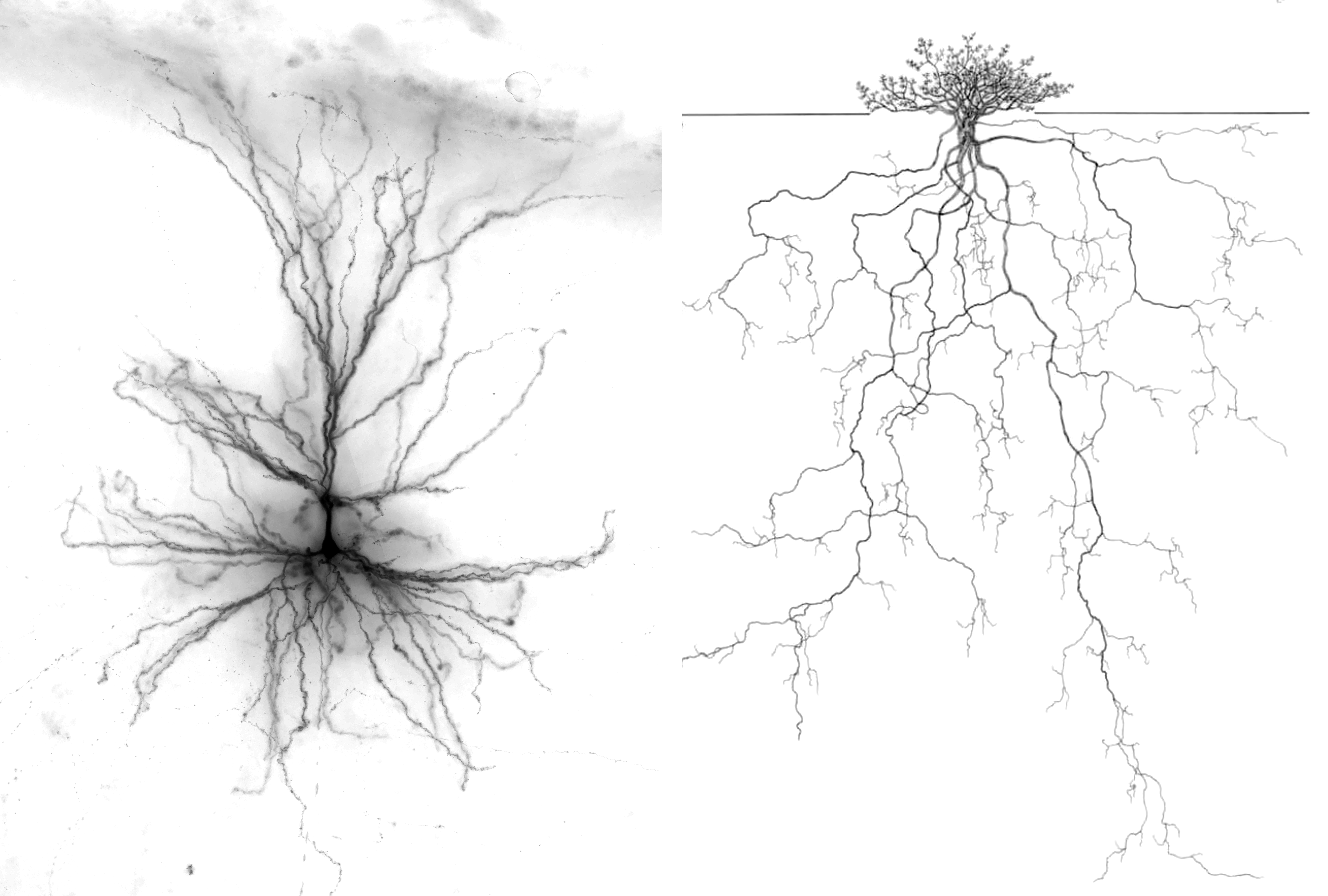
Human neuron in brain and Plant roots in soil
-
VortexNet: Neural Computing through Fluid Dynamics
Abstract

We present VortexNet, a novel neural network architecture that leverages principles from fluid dynamics to address fundamental challenges in temporal coherence and multi-scale information processing. Drawing inspiration from von Karman vortex streets, coupled oscillator systems, and energy cascades in turbulent flows, our model introduces complex-valued state spaces and phase coupling mechanisms that enable emergent computational properties. By incorporating a modified Navier–Stokes formulation—similar to yet distinct from Physics-Informed Neural Networks (PINNs) and other PDE-based neural frameworks—we implement an implicit form of attention through physical principles. This reframing of neural layers as self-organizing vortex fields naturally addresses issues such as vanishing gradients and long-range dependencies by harnessing vortex interactions and resonant coupling. Initial experiments and theoretical analyses suggest that VortexNet supports integration of information across multiple temporal and spatial scales in a robust and adaptable manner compared to standard deep architectures.
Introduction
Traditional neural networks, despite their success, often struggle with temporal coherence and multi-scale information processing. Transformers and recurrent networks can tackle some of these challenges but might suffer from prohibitive computational complexity or vanishing gradient issues when dealing with long sequences. Drawing inspiration from fluid dynamics phenomena—such as von Karman vortex streets, energy cascades in turbulent flows, and viscous dissipation—we propose VortexNet, a neural architecture that reframes information flow in terms of vortex formation and phase-coupled oscillations.
Our approach builds upon and diverges from existing PDE-based neural frameworks, including PINNs (Physics-Informed Neural Networks), Neural ODEs, and more recent Neural Operators (e.g., Fourier Neural Operator). While many of these works aim to learn solutions to PDEs given physical constraints, VortexNet internalizes PDE dynamics to drive multi-scale feature propagation within a neural network context. It is also conceptually related to oscillator-based and reservoir-computing paradigms—where dynamical systems are leveraged for complex spatiotemporal processing—but introduces a core emphasis on vortex interactions and implicit attention fields.
Interestingly, this echoes the early example of the MONIAC and earlier analog computers that harnessed fluid-inspired mechanisms. Similarly, recent innovations like microfluidic chips and neural networks highlight how physical systems can inspire new computational paradigms. While fundamentally different in its goals, VortexNet demonstrates how physical analogies can continue to inform and enrich modern computation architectures.
Core Contributions:
- PDE-based Vortex Layers: We introduce a modified Navier–Stokes formulation into the network, allowing vortex-like dynamics and oscillatory phase coupling to emerge in a complex-valued state space.
- Resonant Coupling and Dimensional Analysis: We define a novel Strouhal-Neural number (Sn), building an analogy to fluid dynamics to facilitate the tuning of oscillatory frequencies and coupling strengths in the network.
- Adaptive Damping Mechanism: A homeostatic damping term, inspired by local Lyapunov exponent spectrums, stabilizes training and prevents both catastrophic dissipation and explosive growth of activations.
- Implicit Attention via Vortex Interactions: The rotational coupling within the network yields implicit attention fields, reducing some of the computational overhead of explicit pairwise attention while still capturing global dependencies.
Core Mechanisms
-
Vortex Layers:
The network comprises interleaved “vortex layers” that generate counter-rotating activation fields. Each layer operates on a complex-valued state space
S(z,t), wherezrepresents the layer depth andtthe temporal dimension. Inspired by, yet distinct from PINNs, we incorporate a modified Navier–Stokes formulation for the evolution of the activation:∂S/∂t = ν∇²S - (S·∇)S + F(x)Here,
νis a learnable viscosity parameter, andF(x)represents input forcing. Importantly, the PDE perspective is not merely for enforcing physical constraints but for orchestrating oscillatory and vortex-based dynamics in the hidden layers. -
Resonant Coupling:
A hierarchical resonance mechanism is introduced via the dimensionless Strouhal-Neural number (Sn):
Sn = (f·D)/A = φ(ω,λ)In fluid dynamics, the Strouhal number is central to describing vortex shedding phenomena. We reinterpret these variables in a neural context:
- f is the characteristic frequency of activation
- D is the effective layer depth or spatial extent (analogous to domain or channel dimension)
- A is the activation amplitude
- φ(ω,λ) is a complex-valued coupling function capturing phase and frequency shifts
- ω represents intrinsic frequencies of each layer
- λ represents learnable coupling strengths
By tuning these parameters, one can manage how quickly and strongly oscillations propagate through the network. The Strouhal-Neural number thus serves as a guiding metric for emergent rhythmic activity and multi-scale coordination across layers.
-
Adaptive Damping:
We implement a novel homeostatic damping mechanism based on the local Lyapunov exponent spectrum, preventing both excessive dissipation and unstable amplification of activations. The damping is applied as:
γ(t) = α·tanh(β·||∇L||) + γ₀Here,
||∇L||is the magnitude of the gradient of the loss function with respect to the vortex layer outputs,αandβare hyperparameters controlling the nonlinearity of the damping function, andγ₀is a baseline damping offset. This dynamic damping helps keep the network in a regime where oscillations are neither trivial nor diverging, aligning with the stable/chaotic transition observed in many physical systems.
Key Innovations
- Information propagates through phase-coupled oscillatory modes rather than purely feed-forward paths.
- The architecture supports both local and non-local interactions via vortex dynamics and resonant coupling.
- Gradient flow is enhanced through resonant pathways, mitigating vanishing/exploding gradients often seen in deep networks.
- The system exhibits emergent attractor dynamics useful for temporal sequence processing.
Expanded Numerical and Implementation Details
To integrate the modified Navier–Stokes equation into a neural pipeline, VortexNet discretizes
S(z,t)over time steps and spatial/channel dimensions. A lightweight PDE solver is unrolled within the computational graph:-
Discretization Strategy: We employ finite differences or
pseudo-spectral methods depending on the dimensionality of
S. For 1D or 2D tasks, finite differences with periodic or reflective boundary conditions can be used to approximate spatial derivatives. - Boundary Conditions: If the data is naturally cyclical (e.g., sequential data with recurrent structure), periodic boundary conditions may be appropriate. Otherwise, reflective or zero-padding methods can be adopted.
-
Computational Complexity: Each vortex layer scales
primarily with
O(T · M)orO(T · M log M), whereTis the unrolled time dimension andMis the spatial/channel resolution. This can sometimes be more efficient than explicitO(n²)attention when sequences grow large. -
Solver Stability: To ensure stable unrolling, we maintain a
suitable time-step size and rely on the adaptive damping mechanism.
If
νorfare large, the network will learn to self-regulate amplitude growth viaγ(t). - Integration with Autograd: Modern frameworks (e.g., PyTorch, JAX) allow automatic differentiation through PDE solvers. We differentiate the discrete update rules of the PDE at each layer/time step, accumulating gradients from output to input forces, effectively capturing vortex interactions in backpropagation.
Relationship to Attention Mechanisms
While traditional attention mechanisms in neural networks rely on explicit computation of similarity scores between elements, VortexNet’s vortex dynamics offer an implicit form of attention grounded in physical principles. This reimagining yields parallels and distinctions from standard attention layers.
1. Physical vs. Computational Attention
In standard attention, weights are computed via:
A(Q,K,V) = softmax(QK^T / √d) VIn contrast, VortexNet’s attention emerges via vortex interactions within
S(z,t):A_vortex(S) = ∇ × (S·∇)SWhen two vortices come into proximity, they influence each other’s trajectories through the coupled terms in the Navier–Stokes equation. This physically motivated attention requires no explicit pairwise comparison; rotational fields drive the emergent “focus” effect.
2. Multi-Head Analogy
Transformers typically employ multi-head attention, where each head extracts different relational patterns. Analogously, VortexNet’s counter-rotating vortex pairs create multiple channels of information flow, with each pair focusing on different frequency components of the input, guided by their Strouhal-Neural numbers.
3. Global-Local Integration
Whereas transformer-style attention has
O(n²)complexity for sequence lengthn, VortexNet integrates interactions through:- Local interactions via the viscosity term
ν∇²S - Medium-range interactions through vortex street formation
- Global interactions via resonant coupling
φ(ω, λ)
These multi-scale interactions can reduce computational overhead, as they are driven by PDE-based operators rather than explicit pairwise calculations.
4. Dynamic Memory
The meta-stable states supported by vortex dynamics serve as continuous memory, analogous to key-value stores in standard attention architectures. However, rather than explicitly storing data, the network’s memory is governed by evolving vortex fields, capturing time-varying context in a continuous dynamical system.
Elaborating on Theoretical Underpinnings
Dimensionless analysis and chaotic dynamics provide a valuable lens for understanding VortexNet’s behavior:
- Dimensionless Groups: In fluid mechanics, groups like the Strouhal number (Sn) and Reynolds number clarify how different forces scale relative to each other. By importing this idea, we condense multiple hyperparameters (frequency, amplitude, spatial extent) into a single ratio (Sn), enabling systematic tuning of oscillatory modes in the network.
-
Chaos and Lyapunov Exponents: The local Lyapunov exponent
measures the exponential rate of divergence or convergence of trajectories
in dynamical systems. By integrating
||∇L||into our adaptive damping, we effectively constrain the system at the “edge of chaos,” balancing expressivity (rich oscillations) with stability (bounded gradients). - Analogy to Neural Operators: Similar to how Neural Operators (e.g., Fourier Neural Operators) learn mappings between function spaces, VortexNet uses PDE-like updates to enforce spatiotemporal interactions. However, instead of focusing on approximate PDE solutions, we harness PDE dynamics to guide emergent vortex structures for multi-scale feature propagation.
Theoretical Advantages
- Superior handling of multi-scale temporal dependencies through coupled oscillator dynamics
- Implicit attention and potentially reduced complexity from vortex interactions
- Improved gradient flow through resonant coupling, enhancing deep network trainability
- Inherent capacity for meta-stability, supporting multi-stable computational states
Reframing neural computation in terms of self-organizing fluid dynamic systems allows VortexNet to leverage well-studied PDE behaviors (e.g., vortex shedding, damping, boundary layers), which aligns with but goes beyond typical PDE-based or physics-informed approaches.
Future Work
-
Implementation Strategies:
Further development of efficient PDE solvers for the modified Navier–Stokes
equations, with an emphasis on numerical stability,
O(n)orO(n log n)scaling methods, and hardware acceleration (e.g., GPU or TPU). Open-sourcing such solvers could catalyze broader exploration of vortex-based networks. -
Empirical Validation:
Comprehensive evaluation on tasks such as:
- Long-range sequence prediction (language modeling, music generation)
- Multi-scale time series analysis (financial data, physiological signals)
- Dynamic system and chaotic flow prediction (e.g., weather or turbulence modeling)
- Architectural Extensions: Investigating hybrid architectures that combine VortexNet with convolutional, transformer, or recurrent modules to benefit from complementary inductive biases. This might include a PDE-driven recurrent backbone with a learned attention or gating mechanism on top.
- Theoretical Development: Deeper mathematical analysis of vortex stability and resonance conditions. Establishing stronger ties to existing PDE theory could further clarify how emergent oscillatory modes translate into effective computational mechanisms. Formal proofs of convergence or stability would also be highly beneficial.
-
Speculative Extensions: Fractal Dynamics, Scale-Free Properties, and Holographic Memory
-
Fractal and Scale-Free Dynamics: One might incorporate wavelet or multiresolution expansions in the PDE solver to natively capture fractal structures and scale-invariance in the data. A more refined “edge-of-chaos” approach could dynamically tune
νandλusing local Lyapunov exponents, ensuring that VortexNet remains near a critical regime for maximal expressivity. - Holographic Reduced Representations (HRR): By leveraging the complex-valued nature of VortexNet’s states, holographic memory principles (e.g., superposition and convolution-like binding) could transform vortex interactions into interference-based retrieval and storage. This might offer a more biologically inspired alternative to explicit key-value attention mechanisms.
-
Fractal and Scale-Free Dynamics: One might incorporate wavelet or multiresolution expansions in the PDE solver to natively capture fractal structures and scale-invariance in the data. A more refined “edge-of-chaos” approach could dynamically tune
Conclusion
We have introduced VortexNet, a neural architecture grounded in fluid dynamics, emphasizing vortex interactions and oscillatory phase coupling to address challenges in multi-scale and long-range information processing. By bridging concepts from partial differential equations, dimensionless analysis, and adaptive damping, VortexNet provides a unique avenue for implicit attention, improved gradient flow, and emergent attractor dynamics. While initial experiments are promising, future investigations and detailed theoretical analyses will further clarify the potential of vortex-based neural computation. We believe this fluid-dynamics-inspired approach can open new frontiers in both fundamental deep learning research and practical high-dimensional sequence modeling.
Code
This repository contains toy implementations of some of the concepts introduced in this research.



-
Eating gamma radiation for breakfast: Some fungal species appear to be able to use strong radiation as an energy source for growth.
Could the fungi be using the extremely high-energy gamma radiation as an energy source in the same way that plants use sunlight?
The key to it all seemed to be melanin – the ubiquitous group of pigments found in many types of eukaryote that protect against UV radiation
Many fungal fossils show evidence of melanisation, especially in periods of high radiation when many animal and plant species died out
Could you replace them with plants or fungi that use melanin instead of chlorophyll?
-
Breakthrough negotiations are underway at the Gnome DeCentral Bank (GDB)