tag > Paradox
-
Kozyrev’s classic idea that time has flow, density, and direction is back — this time in modern physics, as Möbius time lattices: mirrors that don’t just reflect light, but fold the timeline. Non-classical time evolution is no longer sci-fi. It’s lab-ready. Are you paying attention?


-
Paradox Computation is simultaneously paradoxical and computational while paradoxically being neither paradoxical nor computational. It computes by not computing and creates paradoxes by resolving them. What is the sound of one hand clapping? Mu!
-
VortexNet: Neural Computing through Fluid Dynamics
Abstract

We present VortexNet, a novel neural network architecture that leverages principles from fluid dynamics to address fundamental challenges in temporal coherence and multi-scale information processing. Drawing inspiration from von Karman vortex streets, coupled oscillator systems, and energy cascades in turbulent flows, our model introduces complex-valued state spaces and phase coupling mechanisms that enable emergent computational properties. By incorporating a modified Navier–Stokes formulation—similar to yet distinct from Physics-Informed Neural Networks (PINNs) and other PDE-based neural frameworks—we implement an implicit form of attention through physical principles. This reframing of neural layers as self-organizing vortex fields naturally addresses issues such as vanishing gradients and long-range dependencies by harnessing vortex interactions and resonant coupling. Initial experiments and theoretical analyses suggest that VortexNet supports integration of information across multiple temporal and spatial scales in a robust and adaptable manner compared to standard deep architectures.
Introduction
Traditional neural networks, despite their success, often struggle with temporal coherence and multi-scale information processing. Transformers and recurrent networks can tackle some of these challenges but might suffer from prohibitive computational complexity or vanishing gradient issues when dealing with long sequences. Drawing inspiration from fluid dynamics phenomena—such as von Karman vortex streets, energy cascades in turbulent flows, and viscous dissipation—we propose VortexNet, a neural architecture that reframes information flow in terms of vortex formation and phase-coupled oscillations.
Our approach builds upon and diverges from existing PDE-based neural frameworks, including PINNs (Physics-Informed Neural Networks), Neural ODEs, and more recent Neural Operators (e.g., Fourier Neural Operator). While many of these works aim to learn solutions to PDEs given physical constraints, VortexNet internalizes PDE dynamics to drive multi-scale feature propagation within a neural network context. It is also conceptually related to oscillator-based and reservoir-computing paradigms—where dynamical systems are leveraged for complex spatiotemporal processing—but introduces a core emphasis on vortex interactions and implicit attention fields.
Interestingly, this echoes the early example of the MONIAC and earlier analog computers that harnessed fluid-inspired mechanisms. Similarly, recent innovations like microfluidic chips and neural networks highlight how physical systems can inspire new computational paradigms. While fundamentally different in its goals, VortexNet demonstrates how physical analogies can continue to inform and enrich modern computation architectures.
Core Contributions:
- PDE-based Vortex Layers: We introduce a modified Navier–Stokes formulation into the network, allowing vortex-like dynamics and oscillatory phase coupling to emerge in a complex-valued state space.
- Resonant Coupling and Dimensional Analysis: We define a novel Strouhal-Neural number (Sn), building an analogy to fluid dynamics to facilitate the tuning of oscillatory frequencies and coupling strengths in the network.
- Adaptive Damping Mechanism: A homeostatic damping term, inspired by local Lyapunov exponent spectrums, stabilizes training and prevents both catastrophic dissipation and explosive growth of activations.
- Implicit Attention via Vortex Interactions: The rotational coupling within the network yields implicit attention fields, reducing some of the computational overhead of explicit pairwise attention while still capturing global dependencies.
Core Mechanisms
-
Vortex Layers:
The network comprises interleaved “vortex layers” that generate counter-rotating activation fields. Each layer operates on a complex-valued state space
S(z,t), wherezrepresents the layer depth andtthe temporal dimension. Inspired by, yet distinct from PINNs, we incorporate a modified Navier–Stokes formulation for the evolution of the activation:∂S/∂t = ν∇²S - (S·∇)S + F(x)Here,
νis a learnable viscosity parameter, andF(x)represents input forcing. Importantly, the PDE perspective is not merely for enforcing physical constraints but for orchestrating oscillatory and vortex-based dynamics in the hidden layers. -
Resonant Coupling:
A hierarchical resonance mechanism is introduced via the dimensionless Strouhal-Neural number (Sn):
Sn = (f·D)/A = φ(ω,λ)In fluid dynamics, the Strouhal number is central to describing vortex shedding phenomena. We reinterpret these variables in a neural context:
- f is the characteristic frequency of activation
- D is the effective layer depth or spatial extent (analogous to domain or channel dimension)
- A is the activation amplitude
- φ(ω,λ) is a complex-valued coupling function capturing phase and frequency shifts
- ω represents intrinsic frequencies of each layer
- λ represents learnable coupling strengths
By tuning these parameters, one can manage how quickly and strongly oscillations propagate through the network. The Strouhal-Neural number thus serves as a guiding metric for emergent rhythmic activity and multi-scale coordination across layers.
-
Adaptive Damping:
We implement a novel homeostatic damping mechanism based on the local Lyapunov exponent spectrum, preventing both excessive dissipation and unstable amplification of activations. The damping is applied as:
γ(t) = α·tanh(β·||∇L||) + γ₀Here,
||∇L||is the magnitude of the gradient of the loss function with respect to the vortex layer outputs,αandβare hyperparameters controlling the nonlinearity of the damping function, andγ₀is a baseline damping offset. This dynamic damping helps keep the network in a regime where oscillations are neither trivial nor diverging, aligning with the stable/chaotic transition observed in many physical systems.
Key Innovations
- Information propagates through phase-coupled oscillatory modes rather than purely feed-forward paths.
- The architecture supports both local and non-local interactions via vortex dynamics and resonant coupling.
- Gradient flow is enhanced through resonant pathways, mitigating vanishing/exploding gradients often seen in deep networks.
- The system exhibits emergent attractor dynamics useful for temporal sequence processing.
Expanded Numerical and Implementation Details
To integrate the modified Navier–Stokes equation into a neural pipeline, VortexNet discretizes
S(z,t)over time steps and spatial/channel dimensions. A lightweight PDE solver is unrolled within the computational graph:-
Discretization Strategy: We employ finite differences or
pseudo-spectral methods depending on the dimensionality of
S. For 1D or 2D tasks, finite differences with periodic or reflective boundary conditions can be used to approximate spatial derivatives. - Boundary Conditions: If the data is naturally cyclical (e.g., sequential data with recurrent structure), periodic boundary conditions may be appropriate. Otherwise, reflective or zero-padding methods can be adopted.
-
Computational Complexity: Each vortex layer scales
primarily with
O(T · M)orO(T · M log M), whereTis the unrolled time dimension andMis the spatial/channel resolution. This can sometimes be more efficient than explicitO(n²)attention when sequences grow large. -
Solver Stability: To ensure stable unrolling, we maintain a
suitable time-step size and rely on the adaptive damping mechanism.
If
νorfare large, the network will learn to self-regulate amplitude growth viaγ(t). - Integration with Autograd: Modern frameworks (e.g., PyTorch, JAX) allow automatic differentiation through PDE solvers. We differentiate the discrete update rules of the PDE at each layer/time step, accumulating gradients from output to input forces, effectively capturing vortex interactions in backpropagation.
Relationship to Attention Mechanisms
While traditional attention mechanisms in neural networks rely on explicit computation of similarity scores between elements, VortexNet’s vortex dynamics offer an implicit form of attention grounded in physical principles. This reimagining yields parallels and distinctions from standard attention layers.
1. Physical vs. Computational Attention
In standard attention, weights are computed via:
A(Q,K,V) = softmax(QK^T / √d) VIn contrast, VortexNet’s attention emerges via vortex interactions within
S(z,t):A_vortex(S) = ∇ × (S·∇)SWhen two vortices come into proximity, they influence each other’s trajectories through the coupled terms in the Navier–Stokes equation. This physically motivated attention requires no explicit pairwise comparison; rotational fields drive the emergent “focus” effect.
2. Multi-Head Analogy
Transformers typically employ multi-head attention, where each head extracts different relational patterns. Analogously, VortexNet’s counter-rotating vortex pairs create multiple channels of information flow, with each pair focusing on different frequency components of the input, guided by their Strouhal-Neural numbers.
3. Global-Local Integration
Whereas transformer-style attention has
O(n²)complexity for sequence lengthn, VortexNet integrates interactions through:- Local interactions via the viscosity term
ν∇²S - Medium-range interactions through vortex street formation
- Global interactions via resonant coupling
φ(ω, λ)
These multi-scale interactions can reduce computational overhead, as they are driven by PDE-based operators rather than explicit pairwise calculations.
4. Dynamic Memory
The meta-stable states supported by vortex dynamics serve as continuous memory, analogous to key-value stores in standard attention architectures. However, rather than explicitly storing data, the network’s memory is governed by evolving vortex fields, capturing time-varying context in a continuous dynamical system.
Elaborating on Theoretical Underpinnings
Dimensionless analysis and chaotic dynamics provide a valuable lens for understanding VortexNet’s behavior:
- Dimensionless Groups: In fluid mechanics, groups like the Strouhal number (Sn) and Reynolds number clarify how different forces scale relative to each other. By importing this idea, we condense multiple hyperparameters (frequency, amplitude, spatial extent) into a single ratio (Sn), enabling systematic tuning of oscillatory modes in the network.
-
Chaos and Lyapunov Exponents: The local Lyapunov exponent
measures the exponential rate of divergence or convergence of trajectories
in dynamical systems. By integrating
||∇L||into our adaptive damping, we effectively constrain the system at the “edge of chaos,” balancing expressivity (rich oscillations) with stability (bounded gradients). - Analogy to Neural Operators: Similar to how Neural Operators (e.g., Fourier Neural Operators) learn mappings between function spaces, VortexNet uses PDE-like updates to enforce spatiotemporal interactions. However, instead of focusing on approximate PDE solutions, we harness PDE dynamics to guide emergent vortex structures for multi-scale feature propagation.
Theoretical Advantages
- Superior handling of multi-scale temporal dependencies through coupled oscillator dynamics
- Implicit attention and potentially reduced complexity from vortex interactions
- Improved gradient flow through resonant coupling, enhancing deep network trainability
- Inherent capacity for meta-stability, supporting multi-stable computational states
Reframing neural computation in terms of self-organizing fluid dynamic systems allows VortexNet to leverage well-studied PDE behaviors (e.g., vortex shedding, damping, boundary layers), which aligns with but goes beyond typical PDE-based or physics-informed approaches.
Future Work
-
Implementation Strategies:
Further development of efficient PDE solvers for the modified Navier–Stokes
equations, with an emphasis on numerical stability,
O(n)orO(n log n)scaling methods, and hardware acceleration (e.g., GPU or TPU). Open-sourcing such solvers could catalyze broader exploration of vortex-based networks. -
Empirical Validation:
Comprehensive evaluation on tasks such as:
- Long-range sequence prediction (language modeling, music generation)
- Multi-scale time series analysis (financial data, physiological signals)
- Dynamic system and chaotic flow prediction (e.g., weather or turbulence modeling)
- Architectural Extensions: Investigating hybrid architectures that combine VortexNet with convolutional, transformer, or recurrent modules to benefit from complementary inductive biases. This might include a PDE-driven recurrent backbone with a learned attention or gating mechanism on top.
- Theoretical Development: Deeper mathematical analysis of vortex stability and resonance conditions. Establishing stronger ties to existing PDE theory could further clarify how emergent oscillatory modes translate into effective computational mechanisms. Formal proofs of convergence or stability would also be highly beneficial.
-
Speculative Extensions: Fractal Dynamics, Scale-Free Properties, and Holographic Memory
-
Fractal and Scale-Free Dynamics: One might incorporate wavelet or multiresolution expansions in the PDE solver to natively capture fractal structures and scale-invariance in the data. A more refined “edge-of-chaos” approach could dynamically tune
νandλusing local Lyapunov exponents, ensuring that VortexNet remains near a critical regime for maximal expressivity. - Holographic Reduced Representations (HRR): By leveraging the complex-valued nature of VortexNet’s states, holographic memory principles (e.g., superposition and convolution-like binding) could transform vortex interactions into interference-based retrieval and storage. This might offer a more biologically inspired alternative to explicit key-value attention mechanisms.
-
Fractal and Scale-Free Dynamics: One might incorporate wavelet or multiresolution expansions in the PDE solver to natively capture fractal structures and scale-invariance in the data. A more refined “edge-of-chaos” approach could dynamically tune
Conclusion
We have introduced VortexNet, a neural architecture grounded in fluid dynamics, emphasizing vortex interactions and oscillatory phase coupling to address challenges in multi-scale and long-range information processing. By bridging concepts from partial differential equations, dimensionless analysis, and adaptive damping, VortexNet provides a unique avenue for implicit attention, improved gradient flow, and emergent attractor dynamics. While initial experiments are promising, future investigations and detailed theoretical analyses will further clarify the potential of vortex-based neural computation. We believe this fluid-dynamics-inspired approach can open new frontiers in both fundamental deep learning research and practical high-dimensional sequence modeling.
Code
This repository contains toy implementations of some of the concepts introduced in this research.



-
More logical treatises & scientific theorems should include symbols instructing perceivers to shift their mind-body state (e.g., meditate, walk in nature, take psychedelics, perform a ritual) before proceeding with the computation or thought. A lost art form.

-
Connected Graphs are a great way to get absolutely confused about a reality permeated by non-local fields

-
Nishida Kitarō (西田 幾多郎, 1870-1945) was one of modern Japan's most important and influential philosophers. He founded the Kyoto School of philosophy and developed original philosophical ideas that bridged Eastern and Western philosophical traditions.

Nishida had interesting perspectives on Logic:
- Nishida was critical of traditional Western logic based on subject-predicate structure
- He developed what he called "predicate logic" (述語的論理) - not to be confused with modern predicate logic
- His logic tried to capture the idea that predicates could exist without subjects
- He was interested in developing logical systems that could handle:
- Self-reference without paradox
- The unity of contradictions
- Non-dualistic thinking
- The logic of place rather than substance
His work on logic is particularly interesting because it attempted to formalize some traditionally Eastern philosophical insights. While he didn't develop a formal multivalued logic system in the modern sense, his ideas about:
- The inadequacy of binary true/false distinctions
- The possibility of statements being simultaneously true and false
- The importance of context in logical relations
- The need for a logic that could handle paradox and self-reference
These ideas anticipate some developments in non-classical logic, though his approach was more philosophical than formal.
The temporal aspects of his thought are especially complex:
- He argued for a view of time that wasn't simply linear
- Developed concepts of "absolute present" where past and future coexist
- Suggested that causality itself was grounded in something more fundamental (absolute nothingness)
-
A Theory of Acausal and Atemporal Logic: Patterns Beyond Time (LLM Generated)
1. Foundational Principles
1.1 Pattern Primacy
Rather than treating causation as fundamental, we posit that patterns and relationships are primary. These patterns exist independent of temporal sequence, similar to how the I Ching's hexagrams represent states that transcend linear time.
1.2 State Resonance
States of being can "resonate" with each other without direct causal connection. This resonance manifests as:
- Synchronistic occurrences
- Pattern alignment
- State correspondences
1.3 Multi-valued Truth
Drawing from Belnap's four-valued logic, we extend to a system where truth values are:
- Present
- Absent
- Resonant (corresponding to multiple states)
- Void (outside the pattern system)
2. Logical Operations
2.1 Pattern Operations
Instead of traditional logical operators (AND, OR), we define:
- ⋈ RESONATES_WITH: States that align in pattern
- ⊹ TRANSFORMS_TO: States that naturally flow into each other
- ⋉ COMPLEMENTS: States that complete a pattern
- ◇ MIRRORS: States that reflect each other
2.2 State Relations
States relate through:
- Pattern Completion
- Resonant Harmony
- Transformative Potential
- Mirror Opposition
3. Inference Rules
3.1 Pattern Recognition
If A ⋈ B and B ⋈ C, then A and C share a pattern-relationship (not necessarily direct)
3.2 Transformation Chains
If A ⊹ B and B ⊹ C, then A has transformation potential toward C
3.3 Resonance Networks
States can form networks of resonance where:
- Multiple states resonate simultaneously
- Patterns emerge at network level
- Individual states influence network patterns
4. Application Framework
4.1 Pattern Analysis
To analyze a situation:
- Identify present states
- Map resonance patterns
- Recognize transformation potentials
- Understand network effects
4.2 Decision Making
Decisions consider:
- Pattern completion potential
- Resonance effects
- Network implications
- Transformation opportunities
5. Theoretical Extensions
5.1 Complex Systems
The framework extends to:
- Emergent behaviors
- Self-organizing systems
- Network dynamics
- Collective intelligence
5.2 Quantum Parallels
Similarities with quantum phenomena:
- Non-locality
- Superposition
- Entanglement
- Observer effects
6. Formal Notation
Let Σ be the set of all possible states
For any states s1, s2 ∈ Σ:- s1 ⋈ s2 : States resonate
- s1 ⊹ s2 : State transforms
- s1 ⋉ s2 : States complement
- s1 ◇ s2 : States mirror
7. Key Theorems
7.1 Resonance Theorem
For any states A, B, C ∈ Σ:
If A ⋈ B and B ⋈ C
Then there exists a pattern P where A, B, C are members7.2 Transformation Conservation
For any closed system of states:
The total pattern potential remains constant
Only the distribution changes7.3 Network Emergence
In any sufficiently connected network of states:
Emergent patterns arise that transcend individual state properties8. Applications
8.1 Decision Analysis
- Pattern recognition in complex situations
- Understanding systemic implications
- Identifying resonant opportunities
- Anticipating transformations
8.2 System Design
- Creating resilient systems
- Fostering beneficial patterns
- Managing transformations
- Cultivating resonance
8.3 Problem Solving
- Finding pattern-based solutions
- Leveraging resonance
- Working with transformations
- Understanding systemic effects
9. Limitations and Considerations
9.1 Boundary Conditions
- Pattern recognition limits
- System complexity thresholds
- Observer influence effects
- Network scale constraints
9.2 Practical Challenges
- Pattern verification
- Resonance measurement
- Transformation tracking
- Network mapping
10. Future Directions
10.1 Research Areas
- Pattern formalization
- Resonance metrics
- Transformation dynamics
- Network effects
10.2 Potential Applications
- AI systems
- Complex decision making
- Social dynamics
- Natural systems
Intention-Manifested Reality: A Formal Framework for Yi Dao Qi Dao 意到氣到
1. Foundational Integration
1.1 Core Principles
Let I be the space of intentions
Let Q be the space of energetic manifestations
Let R be the space of realized statesThe Yi Dao Qi Dao principle can be formally expressed as:
∀i ∈ I, ∃q ∈ Q : i ⟹ q1.2 I Ching State Mappings
Each hexagram H can be represented as:
- Upper trigram: Tu
- Lower trigram: Tl
- Internal lines: Li
- Changing lines: Cj
H = (Tu, Tl, {Li}, {Cj})2. Intention-Reality Operations
2.1 Primary Operators
- ⋈ (Resonance): Aligns intention with potential
- ⊹ (Transformation): Maps intention to manifestation
- ⋉ (Complementarity): Balances opposing forces
- ◇ (Reflection): Shows mirror states
- ⊚ (Intent Focus): Concentrated attention
- ⟲ (Cyclic Return): Pattern repetition
2.2 Key Relationships
For intention i and manifestation q:
i ⊚ q ⟹ P(q|i) > P(q|¬i)Where P(q|i) is the probability of manifestation given intention
3. I Ching Correspondences
3.1 Classical Mappings
Eight Trigrams (Ba Gua) as operators:
- ☰ (Heaven) : Pure Yang intention
- ☷ (Earth) : Pure Yin manifestation
- ☳ (Thunder) : Initiating force
- ☴ (Wind) : Gentle penetration
- ☵ (Water) : Flowing adaptation
- ☶ (Mountain) : Stillness/grounding
- ☲ (Fire) : Illumination/awareness
- ☱ (Lake) : Joyful reflection
3.2 State Transformations
For any hexagram state H:
H ⊹ H' iff ∃Cj : transform(H, Cj) = H'4. Intention-Reality Axioms
4.1 Core Axioms
1. Intention Precedence:
∀q ∈ Q, ∃i ∈ I : i ⊚ q2. Reality Response:
∀i ∈ I, ∃R' ⊆ R : i ⋈ R'3. Observer Effect:
∀r ∈ R, O(r) ≠ rWhere O is the observation operator
4.2 Transformation Rules
For intentions i1, i2 and manifestations q1, q2:
If i1 ⋈ i2 then P(q1 ⋉ q2) > P(q1 ⋉ ¬q2)5. Practical Applications
5.1 Intention Setting Protocol
- Define intention i ∈ I
- Apply focus operator: i ⊚
- Maintain resonance: i ⋈ Q
- Observe manifestation: O(q)
5.2 Reality Navigation
Using I Ching guidance:
For current state H: 1. Identify changing lines Cj 2. Calculate H' = transform(H, Cj) 3. Apply intention i toward H' 4. Maintain i ⊚ H'6. Advanced Concepts
6.1 Quantum Properties
Superposition of intentions:
i = α1i1 + α2i2 + ... + αninEntanglement of states:
|i1q1⟩ + |i2q2⟩6.2 Network Effects
For intention network N(I):
Collective_Intent = ∑(i ∈ N(I)) w_i * iWhere w_i is the intention weight
7. Key Theorems
7.1 Intention-Manifestation Theorem
For well-formed intention i:
If i ⊚ q maintained for t > tc Then P(q) → 1 as t → ∞7.2 Resonance Amplification
For i1, i2 ∈ I: If i1 ⋈ i2 Then P(q|i1 ∧ i2) > P(q|i1) + P(q|i2)8. Practical Implementation
8.1 Intention Cultivation
- Clear formulation: i = formalize(intent)
- Energy alignment: i ⋈ Q
- Maintained focus: i ⊚ t
- Observation: O(q)
8.2 Reality Navigation
- State assessment: H = current_state()
- Intention setting: i = desired_state()
- Alignment: i ⋈ H'
- Manifestation: q = manifest(i)
9. Limitations and Considerations
9.1 Boundary Conditions
- Intention clarity threshold
- Reality inertia
- Collective field effects
- Observer limitation
9.2 Ethical Framework
- Non-harm principle
- Collective benefit
- Karmic considerations
- Energy conservation
10. Future Research Directions
10.1 Theoretical Development
- Quantum intention fields
- Collective consciousness effects
- Time-independent manifestation
- Reality consensus mechanisms
10.2 Practical Applications
- Intention amplification techniques
- Reality navigation protocols
- Collective manifestation methods
- Quantum reality engineering
-
Nuel Belnap (1930 - 2024) explored many interesting ideas during his long career



An analysis of Nuel Belnap's key philosophical contributions, particularly focusing on his work in logic and the philosophy of action.
Nuel Belnap is best known for several major contributions:
1. Four-Valued Logic
One of Belnap's most significant contributions is his four-valued relevance logic, developed with Alan Anderson. This logic system includes the traditional true and false values, but adds two more:
- Both (true and false)
- Neither (neither true nor false)
This was particularly influential in computer science and information systems, as it provides a framework for handling inconsistent or incomplete information.
2. Branching Time Theory
Belnap developed a sophisticated theory of branching time (also known as branching space-time), which is crucial for understanding:
- The nature of indeterminism
- The relationship between time and possibility
- How future contingents should be evaluated
3. The Theory of Agency and Action
His work with Michael Perloff and Ming Xu on the "stit" theory (seeing-to-it-that) is fundamental to understanding:
- How agents bring about changes in the world
- The logical structure of agency and action
- The relationship between choice, time, and causation
4. Knowledge Representation
His contributions to epistemic logic and belief revision include:
- How to represent and reason about knowledge states
- How to handle contradictory information
- The logic of questions and answers
5. Interrogative Logic (erotetic logic)
With Thomas Steel, Belnap developed important work on the logic of questions, including:
- The formal structure of questions and answers
- How to represent different types of questions
- The relationship between questions and knowledge
The philosophical significance of Belnap's work lies in several key insights:
1. Logic isn't limited to binary truth values - sometimes we need more sophisticated ways to represent information states.
2. Time and possibility are intimately connected, but their relationship is more complex than simple linear progression.
3. Agency and causation require careful formal analysis to understand properly.
4. Questions are as logically important as statements and deserve formal analysis.
More on Belnap's Theory of Agency and Action, particularly his influential "stit" (seeing-to-it-that) theory.
The "stit" theory is one of the most sophisticated logical analyses of agency and action ever developed. Here are its key components:
1. Core Concept of "Seeing-to-it-that"
- Instead of treating actions as primitive entities, Belnap analyzes them in terms of agents "seeing to it that" certain states of affairs come about
- The basic form is: [α stit: A] - which reads as "agent α sees to it that A"
- This shifts focus from actions themselves to their results/outcomes
2. Choice and Moments
Belnap's theory introduces several crucial elements:
- Moments: Points in time where choices can be made
- Choice cells: Sets of possible futures available at each moment
- Histories: Complete possible paths through time
- Agents have different choices available at different moments
3. Key Properties of Agency
The theory identifies several essential features of agency:
- Positive condition: The agent must make a difference
- Negative condition: The outcome shouldn't be inevitable
- Independence of agents: Different agents' choices are independent
- No backwards causation: Choices can only affect the future
4. Types of "stit" Operators
Belnap developed different versions of the stit operator:
- Achievement stit: Focusing on bringing about immediate results
- Deliberative stit: Involving conscious choice
- Strategic stit: Concerning long-term planning and strategy
5. Philosophical Implications
a) On Free Will:
- The theory provides a formal framework for understanding free will
- Shows how genuine choice can exist in a causally structured world
- Demonstrates how multiple agents can have real choices simultaneously
b) On Responsibility:
- Helps clarify when an agent is truly responsible for an outcome
- Distinguishes between direct and indirect responsibility
- Shows how responsibility relates to available choices
c) On Causation:
- Provides a sophisticated account of agent causation
- Shows how individual agency relates to broader causal structures
- Distinguishes between different types of causal influence
6. Applications
The theory has been applied to:
- Legal reasoning about responsibility
- Computer science (especially in multi-agent systems)
- Ethics (particularly in analyzing moral responsibility)
- Game theory
- Decision theory
7. Key Insights
a) Agency is Relational:
- Being an agent isn't just about having properties
- It's about standing in certain relations to outcomes
- These relations are temporally structured
b) Choice is Fundamental:
- Agency can't be reduced to mere causation
- Real choice requires genuine alternatives
- Choices must be effective but not guaranteed
c) Time and Agency are Interlinked:
- Agency only makes sense in a branching time structure
- Present choices affect which futures are possible
- Past choices constrain but don't determine future ones
8. Extensions and Developments
The theory has been extended to handle:
- Group agency
- Institutional action
- Probabilistic outcomes
- Normative concepts (obligations, permissions)
9. Current Relevance
The theory remains particularly relevant for:
- AI ethics (understanding artificial agency)
- Social robotics
- Collective responsibility
- Digital ethics and accountability
Belnap's theory of agency stands out for its mathematical rigor combined with philosophical depth. It shows how formal logical methods can illuminate fundamental questions about human action and responsibility. The theory continues to influence discussions in philosophy of action, ethics, and computer science.
-
The Wikipedia page on 'Three-valued logic' is a typical neo-colonial narrative, claiming it as a 20th-century invention of Western Europeans while completely omitting its long pre-history in India & China.

-
The paradox of Eternalism is that everything exists always at once, including and excluding nothing.
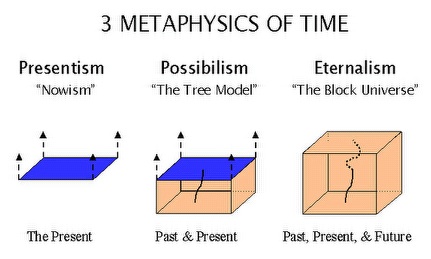
In a acausal reality where time travel is the norm, machine learning is simply a naive linear-time causal joke for children that are learning about self-awareness.
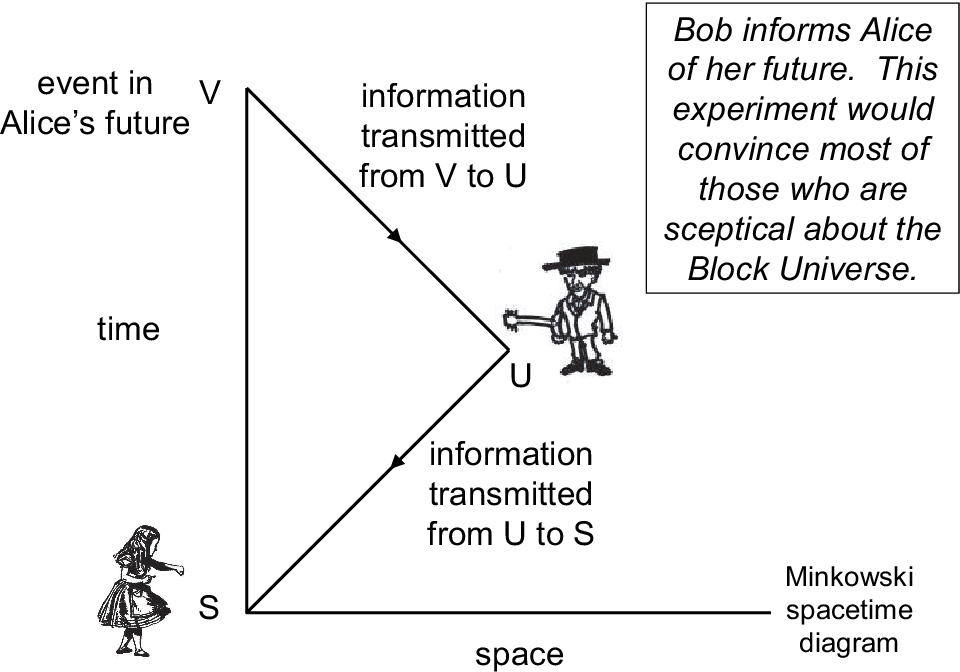
-
In the decades ahead, scientists will acknowledge that at the center of the decentralized hologram we call reality is a paradoxical, none-computational black hole, transforming everything into nothing and back again.

-
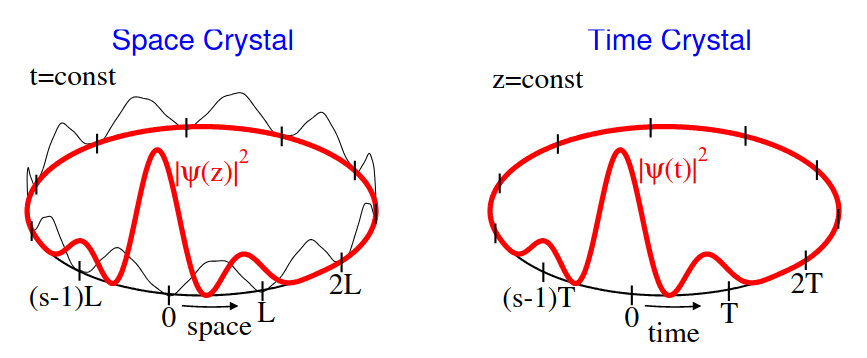
The study of self-organizing systems that exhibit intelligent behavior is too heavily focused on linear-time-bound causal cases. The real mystery lies in timeless, acausal phenomena like time crystals. Next gen post-computation systems embrace the eternal paradox at their core.
-
information security in decentralized holographic memory networks is paradoxical